|
Podemos
esquematizar a axiomatização das geometrias euclidiana e hiperbólica como
segue:
| |
GEOMETRIA ABSOLUTA OU NEUTRA
Termos Primitivos e suas relações
Termos Definidos
Axiomas (exceto o das paralelas)
Teoremas
demonstrados sem o emprego do postulado das paralelas (ou um
equivalente a ele)
|
+ |
Axioma das Paralelas (V Postulado de
Euclides): por um ponto não pertencente a uma reta é possível
traçar uma reta paralela à reta dada. |
= |
|
|
|
GEOMETRIA
EUCLIDIANA |
|
|
| |
+ |
Axioma
das Paralelas: por
um ponto não pertencente a uma reta passam mais de uma reta paralela
à reta dada. |
= |
|
|
|
GEOMETRIA
HIPERBÓLICA |
|
|
David Hilbert (1962-1943) fundamentou a geometria
euclidiana, em sua obra de 1899 chamada de "Fundamentos da
Geometria (1)", através de 21 axiomas, organizados em cinco grupos:
Incidência, Ordem, Congruência, Paralelismo e Continuidade.
Relacionamos no link "RGH" um quadro do método
axiomático de Hilbert, com exceção do axioma de paralelismo, destinados à geometria plana,
que atende o propósito de nosso estudo.
Apresentamos os termos primitivos, as relações não definidas entre os termos
primitivos, os termos definidos, os axiomas e alguns teoremas demonstrados
sem o quinto postulado, que compõem a Geometria Absoluta. Incluímos também
algumas leis que utilizaremos nas demonstrações. Esse quadro resumo será o
ponto de partida para a explanação da geometria hiperbólica em nossa
seqüência didática.
 |
Resumo da
Geometria Absoluta |
É desejável que você observe atentamente o Resumo da
Geometria Absoluta e se familiarize ao conteúdo disponível, pois são as
justificativas possíveis aos passos das demonstrações que serão
apresentadas.
Visando a familiarização da metodologia utilizada nas
demais atividades, para o teorema 01 da Geometria Absoluta, propomos uma construção geométrica,
sua exploração dinâmica, seguida de sua demonstração.
Selecione o botão  e execute as
construções solicitadas, passo a passo. Para cada passo executado
corretamente aparecerá nas instruções a palavra "OK". Para desfazer um passo
utilize o ícone e execute as
construções solicitadas, passo a passo. Para cada passo executado
corretamente aparecerá nas instruções a palavra "OK". Para desfazer um passo
utilize o ícone  . As medidas
dos ângulos e dos lados são dadas respectivamente pelos ícones . As medidas
dos ângulos e dos lados são dadas respectivamente pelos ícones
 e e
 . Selecione o ícone . Selecione o ícone  para mover
os objetos livres da construção. para mover
os objetos livres da construção.
Caso de Congruência de Triângulos: Lado-Ângulo-Lado (LAL)
|
|
Teorema 01: (LAL) Dados os
triângulos ABC e A'B'C' se
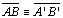 , ,
 e
e
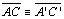 ,
então os triângulos são congruentes. ,
então os triângulos são congruentes. |
|
|
|
|
| No
do Passo |
Passo |
Justificativa |
| 01 |
Dados os
triângulos
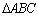 e
e
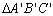 sendo
sendo
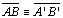 , ,
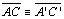 e
e
 . . |
Hipótese |
| 02 |
Temos
que
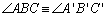 . . |
01,
C 05 |
| 03 |
Vamos
supor
que
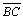 não seja congruente a
não seja congruente a
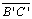 ,
ou seja, ,
ou seja, 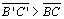 (podemos
provar o mesmo supondo (podemos
provar o mesmo supondo
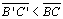 ). ). |
Negação da
Tese |
| 04 |
|
T 16;
C 01, Construção |
| 05 |
Temos que
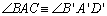 ,
pois ,
pois
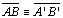 (hipótese),
(hipótese), 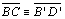 (passo
4) e (passo
4) e 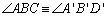 (passo 2). (passo 2). |
01; 02; 04; C 05 |
| 06 |
Contradição, pois
 (hipótese) e (hipótese) e
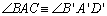 (passo
05), o que é impossível pois o transporte de um ângulo a partir de uma
semi-reta, no mesmo semi-plano, só pode ser feito de uma única maneira. (passo
05), o que é impossível pois o transporte de um ângulo a partir de uma
semi-reta, no mesmo semi-plano, só pode ser feito de uma única maneira. |
01, 05,
C 04 |
| 07 |
Refazendo
os passos 03-06 para
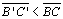 encontramos
também uma contradição. Portanto encontramos
também uma contradição. Portanto
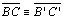 . . |
06 |
| 08 |
Temos
que 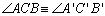 , pois , pois
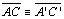 (hipótese),
(hipótese),
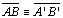 (hipótese) e
(hipótese) e 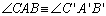 (hipótese).
(hipótese). |
01,
C 05 |
| 09 |
Os
triângulos
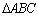 e
e
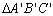 apresentam respectivamente os lados e os ângulos respectivamente
congruentes, logo
apresentam respectivamente os lados e os ângulos respectivamente
congruentes, logo  . . |
01; 02;
05; 07; 08 |
Perceba que o T 01 não utilizou o axioma das paralelas em
sua demonstração, sendo portanto um teorema da geometria absoluta, válido
tanto para a geometria euclidiana como a geometria hiperbólica.
|
 e
e
 . Selecione o ícone
. Selecione o ícone 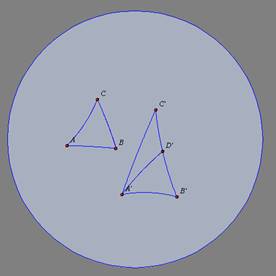
 (passo
4) e
(passo
4) e  (passo 2).
(passo 2).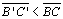 encontramos
também uma contradição. Portanto
encontramos
também uma contradição. Portanto
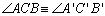 , pois
, pois
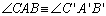 (hipótese).
(hipótese).