|
|
|
Definição
Hiperbólica 05: Se dos extremos de um segmento de reta
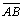 forem traçadas duas retas paralelas assintóticas num determinado
sentido e se tomarmos um ponto qualquer de cada reta posicionados no
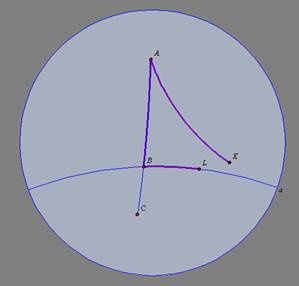
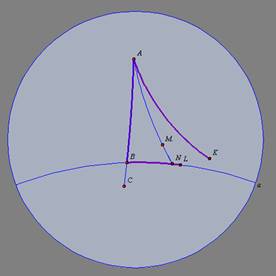
lado do paralelismo (K e L), então a figura KABL é dita biângulo e o
segmento dado é a sua base.
forem traçadas duas retas paralelas assintóticas num determinado
sentido e se tomarmos um ponto qualquer de cada reta posicionados no
lado do paralelismo (K e L), então a figura KABL é dita biângulo e o
segmento dado é a sua base.
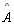 e
e
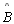 são os ângulos.
são os ângulos.
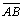 é a base.
é a base.
OBS: Note que WABM não é um biângulo, pois os pontos
W e M estão situados no sentido oposto ao do paralelismo. |
 |
TH 11:
Em um biângulo, o ângulo externo é maior que o ângulo interno oposto, ou
seja,
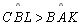 |
|
Demonstração |
Hipótese: Seja KABL um biângulo, conforme a figura. Prolongando a
base
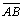 até um ponto qualquer C, temos o ângulo externo
até um ponto qualquer C, temos o ângulo externo
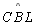 |
|
Tese:
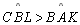 |
| No do
Passo |
Passo |
Justificativa |
|
01 |
Seja KABL
um biângulo, conforme a figura. Prolongando a base
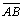 até um ponto qualquer C temos o ângulo externo
até um ponto qualquer C temos o ângulo externo
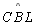 |
Hipótese |
|
02 |
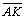 e
e
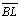 são
paralelas assintóticas no sentido do paralelismo (no caso, à direita) são
paralelas assintóticas no sentido do paralelismo (no caso, à direita) |
DH 05 |
|
03
|
Demonstraremos que
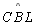 não é menor que
não é menor que
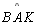 |
-
Suponhamos
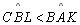
|
Negação da
tese |
|
|
C 04; construção |
-
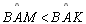
|
03.1;
03.2, P 07 |
-
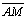 passa pela região angular KAB
passa pela região angular KAB
|
03.3 |
-
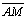 é secante à reta
é secante à reta
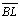
|
02; 03.4;
DH 03 |
 |
- Prolonguemos
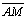 até que se intersecte com
até que se intersecte com
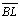 no ponto N
no ponto N
|
|
O 02
;Construção;Ct 01 |
- No
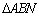 temos que
temos que
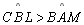
|
T 08 |
- Contradição. Logo
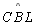 não é menor que
não é menor que
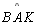
|
03.2; 03.7 |
|
04 |
Demonstraremos que
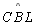 não é congruente a
não é congruente a
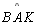 |
-
Suponhamos
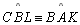
|
Negação da
tese |
|
|
D
17;T 02;O 02; C 01; Construção;I 01 |
|
2.a
Verificaremos se os pontos Q, O e P são alinhados: |
|
2.a.1
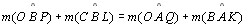 |
T 03;
P 01 |
|
2.a.2
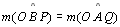 |
04.1;
04.2.a.1; P 25 |
|
2.a.3
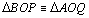 ,
pois ,
pois
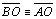 (04.2),
(04.2),
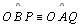 (04.2.a.2)
e (04.2.a.2)
e
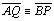 (04.2) (04.2) |
T 01 |
|
2.a.4
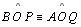 |
04.2.a.3 |
|
2.a.5
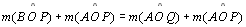 |
04.2.a.4;
P 08 |
|
2.a.6
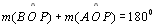 |
T 03 |
|
2.a.7
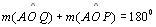 |
04.2.a.5;
04.2.a.6; P 01 |
|
2.a.8
Logo os pontos Q, O e P são alinhados |
T 09 |
-
Temos
que
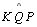 é
reto é
reto
|
04.2.a.3 |
-
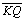 é
paralela assintótica a é
paralela assintótica a
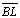 por Q
por Q
|
02;
TH 04 |
-
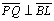
|
04.2;
04.2.a.8 |
-
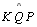 é agudo
é agudo
|
TH 03;04.4 |
-
Contradição. Logo
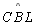 não é congruente a
não é congruente a
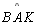
|
04.3; 04.6 |
| 05 |
Temos
então que
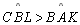 ,
pois ,
pois 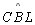 não é menor
nem congruente a não é menor
nem congruente a
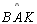 . . |
03.8;
04.7; P 09 |
|
Demonstre o TH12 negando a tese (considere como
hipótese uma das relações válidas, e prove que d ║a. Em seguida, negue a
tese supondo a e d paralelas assintóticas à direita e depois à esquerda
chegando a contradições). |
Resposta |
|
CASOS DE CONGRUÊNCIA DOS
BIÂNGULOS |
|
 |
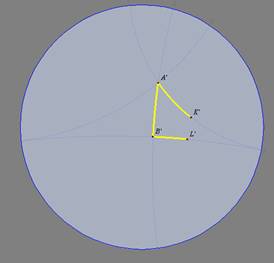 |
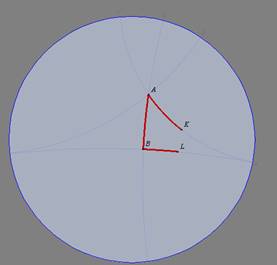
TH 13: (A-B) Se dois biângulos apresentam um ângulo interno e a
base congruentes, então eles são congruentes.
Se
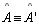 e
e
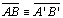 ,
então ,
então
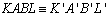
ou
Se
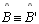 e
e
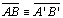 ,
então ,
então
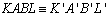
|
|
Demonstração |
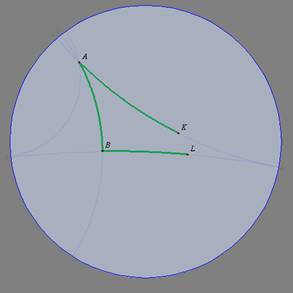
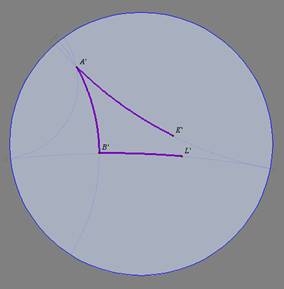
Hipótese: Sejam os biângulos KABL e K'A'B'L', com
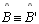 e
e
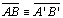 |
|
Tese:
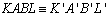 |
| No do
Passo |
Passo |
Justificativa |
| 01 |
Sejam os
biângulos KABL e K'A'B'L', com
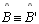 e
e
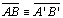 |
Hipótese |
| 02 |
Vamos
supor que os biângulos não sejam congruentes, ou seja, os ângulos
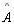 e
e
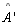 não são congruentes. Vamos considerar
não são congruentes. Vamos considerar
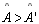 (
(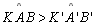 ). Deve-se
provar o mesmo para ). Deve-se
provar o mesmo para
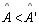 . . |
Negação da
Tese |
| 03 |
|
C 04; construção |
| 04 |
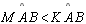 e portanto
e portanto
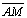 está
na região angular KAB está
na região angular KAB |
02; 03;
P 10 |
| 05 |
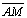 é
secante à reta é
secante à reta
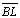 |
01, 04;
DH 03 |
| 06 |
|
O 02;
construção; Ct 01 |
| 07 |
|
C01; construção |
| 08 |
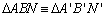 ,
pois ,
pois
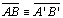 (hipótese), (hipótese),
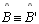 (hipótese) e
(hipótese) e 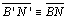 (07) (07)
|
T 01; 01; 07 |
| 09 |
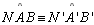 ,
( ou ,
( ou
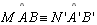 ) ) |
08 |
| 10 |
Consequentemente temos
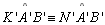 |
03; 09;
P 01 |
| 11 |
Mas
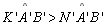 |
P 04 |
| 12 |
Contradição. Logo
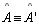 |
10;11 |
| 13 |
Analogamente, podemos considerar como hipótese que
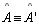 e concluir que e concluir que
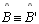 . . |
01-12 |
| 14 |
Logo
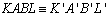 |
12, 13 |
|
 |
 |
TH 14: (A-A) Se dois biângulos apresentam os ângulos
correspondentes congruentes, então eles são congruentes.
Se
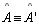 e
e
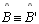 ,
então ,
então
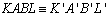
|
| No do
Passo |
Passo |
Justificativa |
| 01 |
Sejam os
biângulos KABL e K'A'B'L', com
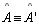 (
(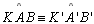 )
e )
e
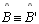 ( (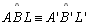 ) ) |
Hipótese |
| 02 |
Vamos
supor que os biângulos não sejam congruentes, ou seja, os segmentos
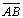 e
e
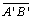 não são congruentes. Vamos considerar não são congruentes. Vamos considerar
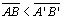 .Deve-se
provar o mesmo para .Deve-se
provar o mesmo para
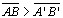 . . |
Negação da
Tese |
| 03 |
|
C 01; construção |
| 04 |
|
AH 01;
construção |
| 05 |
Conseqüentemente
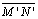 é
paralela assintótica à direita, também em relação à reta é
paralela assintótica à direita, também em relação à reta
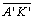 |
TH 07 |
| 06 |
K'A'M'N' e
N'M'B'L' são biângulos |
05
(K'A'M'N' ); 04 (N'M'B'L');
DH 05 |
| 07 |
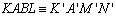 ,
pois ,
pois
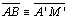 (construção) e
(construção) e
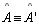 (hipótese). Logo
(hipótese). Logo
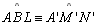 |
06;
TH 13 |
| 08 |
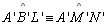 |
01,07,
P 01 |
| 09 |
No
biângulo N'M'B'L' temos que
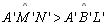 |
TH 11 |
| 10 |
Contradição. Logo
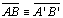 |
08 ; 09 |
| 11 |
Nessas
condições temos que
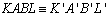 |
01,10 |
Após a atividade 6, o Resumo foi atualizado.
 |
Resumo da Geometria
Hiperbólica (RGH) |
|