|
|
Definição
Hiperbólica 06: Um quadrilátero de Saccheri é um quadrilátero no
qual dois de seus lados opostos são congruentes e apresentam uma
perpendicular comum que é um outro seu lado, chamado de base.O lado
oposto à base é chamado topo.
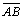 :
base (perpendicular comum à :
base (perpendicular comum à
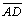 e
e
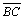 ) )
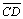 :
topo :
topo
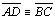 :
lados opostos congruentes :
lados opostos congruentes
Ângulos da base: 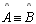 (retos)
(retos)
Ângulos do topo:
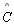 e
e
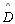 |
| No do
Passo |
Passo |
Justificativa |
| 01 |
Seja □ABCD
um quadrilátero de Saccheri, sendo
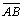 a base e seja K e L os pontos médios respectivamente de
a base e seja K e L os pontos médios respectivamente de
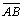 e e 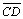 . . |
Hipótese |
|
02 |
Demonstraremos que os ângulos da base são congruentes (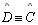 ou ou
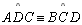 )
) |
|
|
Construção;
I 01 |
-
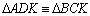 ,
pois ,
pois
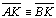 (hipótese);
(hipótese);
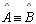 (def. quadrilátero de Saccheri) e
(def. quadrilátero de Saccheri) e
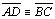 (def.
quadrilátero de Saccheri) (def.
quadrilátero de Saccheri)
|
T 01 |
-
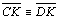 e
e 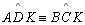
|
02.2 |
-
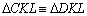 ,
pois ,
pois
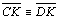 (02.3);
(02.3);
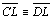 (hipótese)
e (hipótese)
e
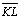 (comum) (comum)
|
T 10 |
-
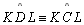
|
02.4 |
-
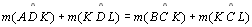
|
02.3;
02.5; P 11 |
-
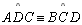
|
02.6 |
|
03 |
Demonstraremos que
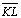 é
perpendicular à base é
perpendicular à base
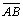 |
-
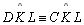 , ,
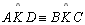
|
02.2;
02.4; |
-
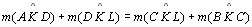
|
03.1;
P 11 |
-
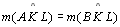
|
03.2 |
-
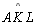 e e
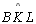 são congruentes e suplementares
são congruentes e suplementares
|
03.3;
D 06 |
-
Logo
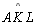 e
e
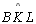 são retos
são retos
|
03.4;
T 03 |
-
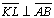
|
03.5;
D 13 |
| 04 |
Demonstraremos que
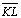 é
perpendicular ao topo é
perpendicular ao topo
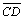 |
| 05 |
-
Da mesma
forma, como
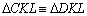 ,
prova-se que os ângulos ,
prova-se que os ângulos
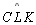 e e
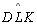 são
congruentes e retos. Logo são
congruentes e retos. Logo
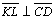 . .
|
02.4;
D 06 ;D 13 |
|
|
TH 16: A base e o topo de um quadrilátero de Saccheri são
paralelas divergentes, e também o são os outros dois lados.
|
|
Demonstre o TH 16. Você vai precisar do teorema TH
15. |
Resposta |
|
|
TH 17: Os ângulos do topo de um quadrilátero de Saccheri são
agudos
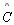 e
e 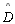 são agudos
são agudos
|
|
Demonstração |
Hipótese: Seja □ABCD um quadrilátero de Saccheri, sendo
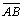 a base
a base |
|
Tese:
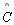 e
e
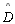 são agudos
são agudos |
| No do
Passo |
Passo |
Justificativa |
| 01 |
Seja □ABCD
um quadrilátero de Saccheri, onde
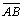 é a base
é a base |
Hipótese |
| 02 |
|
DH 03; construção |
| 03 |
Verificaremos se
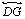 e
e
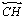 estão
sob a reta DCE estão
sob a reta DCE |
-
DCE é
paralela divergente a ABF por D
|
01; TH 16 |
-
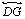 é paralela assintótica a ABF por D
é paralela assintótica a ABF por D
|
02 |
-
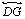 está no espaço angular EDA
está no espaço angular EDA
|
DH 03; 03.2 |
-
Analogamente
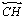 está no espaço angular ECB
está no espaço angular ECB
|
03.1-03.3
|
| 04 |
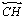 e
e
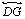 são paralelas assintóticas entre elas no mesmo sentido em que são
paralelas assintóticas em relação à
são paralelas assintóticas entre elas no mesmo sentido em que são
paralelas assintóticas em relação à
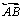 (no caso, à direita)
(no caso, à direita) |
TH 07 |
| 05 |
Logo □HCDG
é um biângulo de base
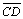 |
04;
DH 05 |
| 06 |
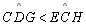 |
TH 11 |
| 07 |
□GDAF e □HCBF
são biângulos |
02;
DH 05 |
| 08 |
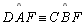 (retos)
e (retos)
e
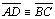 |
01;
DH 06 |
| 09 |
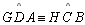 .
(A-B) pois, .
(A-B) pois,
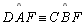 e
e 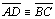 |
08,
TH 13 |
| 10 |
Por 06
temos que
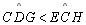 .
Somando .
Somando
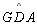 em ambos os membros, temos que
em ambos os membros, temos que
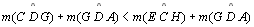 ,
ou ainda podemos substituir ,
ou ainda podemos substituir
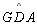 por
por
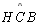 (por 09), obtendo
(por 09), obtendo
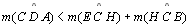 .
Ou seja, .
Ou seja,
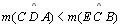 |
06; 09;
P 12 |
| 11 |
Mas
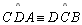 |
01, TH 15 |
| 12 |
Então
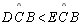 |
10, 11,
P 07 |
| 13 |
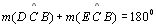 |
T 03 |
| 14 |
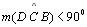 |
12, 13,
P 13 |
| 15 |
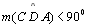 |
11, 14,
P 14 |
| 16 |
Logo,
como 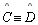 , temos que , temos que
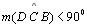 |
TH 15 |
|
|
Analise a seguinte situação:
os quadriláteros de Saccheri existem na geometria euclidiana.
Se tomarmos a definição tradicional de retângulo
euclidiano, ou seja, a de um quadrilátero plano convexo que apresenta os
quatro ângulos congruentes, teremos os retângulos na geometria hiperbólica? Explore dinamicamente a
figura, mantendo o ponto D no interior do plano de Poincaré. |
Resposta |
Após a atividade 7, o Resumo foi atualizado.
 |
Resumo da Geometria
Hiperbólica (RGH) |
|