|
Construa um triângulo, determine a medida
de seus ângulos (escolha o ícone  e marque os
lados do ângulo) e em seguida investigue dinamicamente como se comporta a
soma das medidas de seus ângulos. e marque os
lados do ângulo) e em seguida investigue dinamicamente como se comporta a
soma das medidas de seus ângulos.
|
|
|
|
|
|
TH 24: A soma dos ângulos internos de um triângulo
 é menor que
180o, ou seja, é menor que
180o, ou seja,
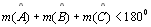
|
|
Demonstração |
Hipótese: Dado um triângulo qualquer
 |
|
Tese:
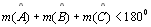 |
| No do
Passo |
Passo |
Justificativa |
| 01 |
Dado um
triângulo
 |
Hipótese |
| 02 |
|
Construção;
T 02;
D 17 |
| 03 |
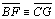 |
T 12 (2.) |
| 04 |
O quadrilátero □GFBC é um quadrilátero de Saccheri,
sendo
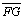 a base
a base |
02; 03;
DH 06 |
| 05 |
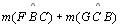 é igual a soma dos ângulos internos de
é igual a soma dos ângulos internos de
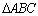 |
T 12 (3.) |
| 06 |
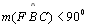 e
e
 |
TH 17 |
| 07 |
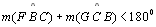 |
06;
P 19 |
| 08 |
Portanto a
soma dos ângulos internos de um triângulo é menor que 180o. |
05; 07;
P 20 |
|
Demonstre o teorema TH 25 que é conseqüência imediata do TH 24. |
Resposta |
|
TH 25: A soma dos ângulos internos de um
quadrilátero □ABCD
é menor que 360o, ou seja,
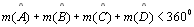 . .
|
|
CASO DE CONGRUÊNCIA DOS
TRIÂNGULOS |
|
TH 26: (AAA) Se dois triângulos apresentam respectivamente iguais os
três ângulos internos, então os triângulos são congruentes |
|
Demonstração |
Hipótese: Sejam os triângulos
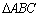 e
e
 com os respectivos ângulos congruentes
com os respectivos ângulos congruentes |
|
Tese:
 |
| No do
Passo |
Passo |
Justificativa |
| 01 |
Sejam os
triângulos
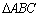 e
e
 com os respectivos ângulos congruentes, ou seja
com os respectivos ângulos congruentes, ou seja
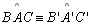 , ,
 e
e
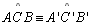 . . |
Hipótese |
| 02 |
Vamos
supor que os triângulos sejam semelhantes, mas não congruentes, ou seja,
seus respectivos lados não são congruentes. |
Negação da
tese |
| 03 |
|
C 01;
C 04; construção;
T 16 |
|
04 |
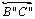 intersecta
intersecta
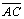 em C''. Vamos provar que C'' está em
em C''. Vamos provar que C'' está em
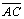 |
O 04 |
-
C'' não
está em
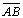 ,
pois caso contrário haveria duas retas que ligaria B'' a C''. ,
pois caso contrário haveria duas retas que ligaria B'' a C''.
|
I 02 |
-
 é paralela a
é paralela a
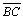
|
01; 03;
TH 12 |
-
C'' não
está em
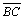
|
04.2;
DH 01 |
-
Logo C''
está em
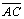
|
04.1; 04.3 |
| 05 |
Por 01 temos
 .
Por 03 temos .
Por 03 temos
 .
Logo .
Logo
 |
01; 03;
P 01 |
| 06 |
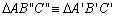 ,
pois ,
pois
 (por 05);
(por 05);
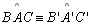 (por 01) e
(por 01) e
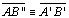 (por 3)
(por 3) |
T 11;01; 03; 05 |
| 07 |
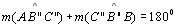 |
T 03 |
| 08 |
Por 03
temos
 .Por
07 temos .Por
07 temos
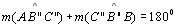 .
Logo .
Logo
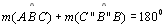 |
03; 07;
P22 |
| 09 |
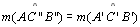 |
06 |
| 10 |
Por 01
temos
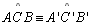 .
Por 09 temos .
Por 09 temos
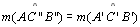 .
Logo .
Logo
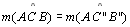 |
01; 09;
P 01 |
| 11 |
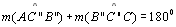 |
T 03 |
| 12 |
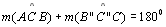 |
10; 11;
P 22 |
| 13 |
Somando as
equações temos:
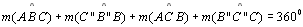 |
08; 12;
P 21 |
| 14 |
Temos
então um quadrilátero □BCC''B'' cuja soma dos ângulos internos é igual a
360o. |
13 |
| 15 |
Contradição, pois tal quadrilátero não existe na geometria hiperbólica.
Portanto os triângulos são congruentes. |
09;
T 25 |
|
 |
TH 27: A medida de um ângulo externo de um triângulo é maior que
a soma das medidas dos lados não adjacentes a ele.

|
|
Demonstração |
Hipótese: Dado um triângulo
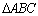 e sendo
e sendo
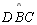 um
seu ângulo externo um
seu ângulo externo |
|
Tese: |
| No do
Passo |
Passo |
Justificativa |
| 01 |
Seja o
triângulo
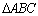 e
e
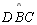 um seu ângulo externo.
um seu ângulo externo. |
Hipótese |
| 02 |
 (
(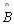 ou ou
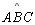 ) )
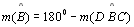 |
T 03 |
| 03 |
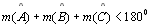 |
TH 24 |
| 04 |
Substituindo 02 em 03 temos:
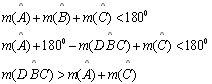 |
02; 03 |
|
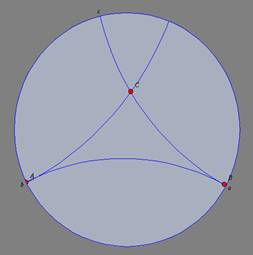
A geometria hiperbólica permite a existência de
triângulos com um ou mais vértices em
pontos ideais. São os chamados triângulos ômega (DH 08).
|
|
um vértice num ponto ideal |
dois
vértices em pontos ideais |
três
vértices em pontos ideais |
|
 |
 |
 |
Após a atividade 9, o Resumo foi atualizado.
 |
Resumo da Geometria
Hiperbólica (RGH) |
|