|
|
TH 29: As três retas
perpendiculares nos pontos médios aos lados de um triângulo ou passam
por um mesmo ponto, ou são paralelas divergentes ou paralelas
assintóticas num mesmo sentido. |
|
Demonstração |
Hipótese: Seja o triângulo
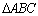 de lados de lados
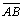 , ,
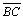 e e
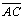 e
pontos médios respectivamente M, N, L. e
pontos médios respectivamente M, N, L. |
|
Tese: Ou as retas perpendiculares à M, N e
L passam por um mesmo ponto I (caso 1); ou são paralelas divergentes
(caso 2) ou são paralelas assintóticas num mesmo sentido (caso 3). |
| No do
Passo |
Passo |
Justificativa |
|
01 |
Seja o
triângulo ABC de lados
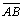 , ,
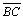 e e
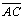 e pontos
médios respectivamente M, N, L. e pontos
médios respectivamente M, N, L. |
Hipótese |
|
02 |
Tracemos as perpendiculares à
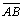 por M e à por M e à
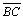 por N. por N.
|
Construção; T 02 |
|
03 |
|
Essas perpendiculares podem sem: secantes,
paralelas divergentes ou ou paralelas assintóticas num mesmo sentido |
DH 03 |
|
04
|
|
1o Caso: as perpendiculares à
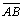 por M e à por M e à
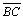 por N
são secantes e se intersectam num ponto I. por N
são secantes e se intersectam num ponto I.
|
|
04.1.Tracemos
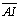 e e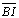
|
Construção; I 01 |
|
04.2.
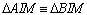 , pois , pois
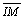 é comum, é comum,
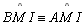 (retos) e (retos) e
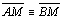 (M é ponto
médio de (M é ponto
médio de 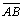 ) ) |
T 01 |
|
04.3. Logo
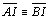 |
04.2. |
|
04.4. Tracemos
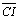 |
Construção; I 01 |
|
04.5.
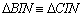 , pois , pois
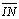 é comum, é comum,
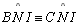 (retos) e (retos) e
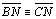 |
T 01 |
|
04.6. Logo
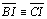 |
04.5 |
|
04.7.Temos então que
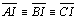 , ou seja I é
eqüidistante dos vértices do triângulo. , ou seja I é
eqüidistante dos vértices do triângulo. |
04.3, 04.6 e
P 01 |
|
Obs: Note que o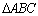 é inscritível na circunferência de centro I (D
22 e 04.7)
é inscritível na circunferência de centro I (D
22 e 04.7) |
|
05 |
|
2o
Caso: as perpendiculares à
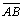 por M e à por M e à
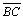 por N
são paralelas divergentes por N
são paralelas divergentes |
|
05.1. As perpendiculares à
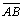 por M e à por M e à
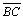 por N
apresentam uma perpendicular comum por N
apresentam uma perpendicular comum
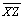 |
TH 09 |
|
05.2. Tracemos H na intersecção da perpendicular
à 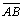 com com
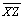 e tracemos K na
intersecção da perpendicular à e tracemos K na
intersecção da perpendicular à
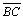 com com
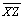 . . |
Construção |
|
05.3. Tracemos o ponto médio de
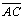 , denominando-o
de L. Tracemos a perpendicular à , denominando-o
de L. Tracemos a perpendicular à
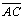 por L. por L. |
Construção; T 02 |
|
05.4. Tracemos por A, B e C as perpendiculares à
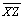 , que a
encontram respectivamente nos pontos D , E e F. , que a
encontram respectivamente nos pontos D , E e F. |
Construção; T 02 |
|
05.5.
 , pois , pois
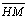 é comum, é comum,
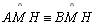 (retos) e (retos) e
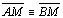 (M é ponto
médio de (M é ponto
médio de 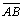 ) ) |
T 01 |
|
05.6.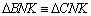 ,
pois ,
pois 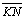 é comum, é comum,
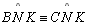 (retos) e (retos) e
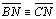 (N é ponto
médio de (N é ponto
médio de 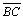 ) ) |
T 01 |
|
05.7.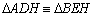 ,
pois ,
pois 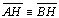 (por
05.5), (por
05.5), 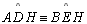 (retos)
e (retos)
e 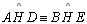 (por 05.5 e
D 23) (por 05.5 e
D 23) |
T 15 |
|
05.8. Logo
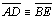 |
05.7 |
|
05.9.
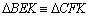 , pois , pois
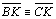 (por 05.6), (por 05.6),
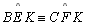 (retos) e (retos) e
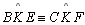 (por 05.6 e
D 23) (por 05.6 e
D 23) |
T 15 |
|
05.10. Logo
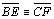 |
05.9 |
|
05.11. Temos então que
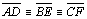 , ou seja, os
vértices do triângulo são eqüidistantes da perpendicular comum , ou seja, os
vértices do triângulo são eqüidistantes da perpendicular comum
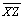 . . |
05.8 e 05.10 e P
01 |
|
05.12. O
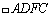 é um
quadrilátero de Saccheri, de base é um
quadrilátero de Saccheri, de base
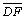 . . |
DH
06 e 05.11 |
|
05.13. Tracemos pelo ponto médio L, de
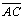 , uma
perpendicular que encontra , uma
perpendicular que encontra
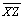 em P em P |
Construção |
|
05.14.
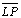 é
perpendicular à é
perpendicular à 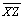 |
TH
15 |
|
05.15. Logo as paralelas pelos pontos
médios dos lados do
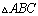 , ou seja , ou seja
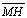 , ,
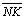 e e
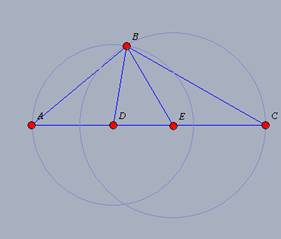
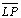 , são
perpendiculares à reta , são
perpendiculares à reta
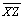 . Logo são
paralelas divergentes. . Logo são
paralelas divergentes. |
TH
12 |
|
06 |
|
3o
Caso: as perpendiculares à
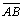 por M e à por M e à
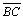 por N
são paralelas assintóticas num mesmo sentido. por N
são paralelas assintóticas num mesmo sentido. |
|
Vamos provar inicialmente que a terceira
perpendicular é paralela assintótica |
|
06.1. Supondo que a terceira reta, perpendicular
à
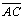 , por L, seja
concorrente com a perpendicular à , por L, seja
concorrente com a perpendicular à
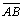 por M. Sendo
assim será concorrente também com a perpendicular à por M. Sendo
assim será concorrente também com a perpendicular à
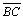 por N, o que
contraria a hipótese do 3O caso. por N, o que
contraria a hipótese do 3O caso. |
04 (Caso 1) |
|
06.2. Supondo que a terceira reta, perpendicular
à
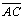 , por L,
tenha uma perpendicular comum com a perpendicular à , por L,
tenha uma perpendicular comum com a perpendicular à
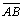 por M. Sendo
assim terá também uma perpendicular comum com a perpendicular à por M. Sendo
assim terá também uma perpendicular comum com a perpendicular à
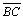 por N, o que
contraria a hipótese do 3O caso. por N, o que
contraria a hipótese do 3O caso. |
05 (Caso 2) |
|
06.3. Logo a perpendicular à
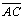 , por L é uma
paralela assintótica. , por L é uma
paralela assintótica. |
06.1. e 06.2 |
|
Vamos provar que as três perpendiculares
apresentam uma transversal comum (ou seja, elas não determinam um
triângulo com seus vértices em pontos ideais), sendo portanto
paralelas assintóticas no mesmo sentido. |
|
|
Construção; C 04 |
|
06.5. Os triângulos
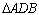 e e
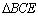 são isósceles,
com são isósceles,
com 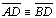 e e 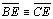 . . |
06.4 e D
16 |
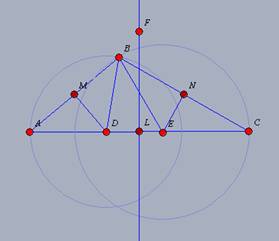 |
06.6. Tracemos os pontos médios M, N e L,
respectivamente dos lados
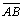 , ,
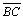 e e
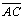 . Tracemos as
perpendiculares à . Tracemos as
perpendiculares à
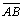 por M e à por M e à
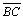 por N, que
encontram por N, que
encontram 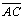 respectivamente em D e E. Tracemos por L uma perpendicular à
respectivamente em D e E. Tracemos por L uma perpendicular à
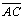 . . |
|
Construção, 06.5 e
D 24 |
|
06.7. As perpendiculares ao lados pelos seus
pontos médios apresentam uma transversal comum
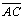 . Logo são
paralelas assintóticas num mesmo sentido. . Logo são
paralelas assintóticas num mesmo sentido. |
06.6 |
Na Geometria Hiperbólica temos três tipos de feixes de
retas:
|
Caso 1: feixe constituído de todas as retas do plano passando
por um ponto, dito centro do feixe (O). |
Caso 2: feixe "próprio" constituído de todas as retas do plano
perpendiculares à uma mesma reta (a), dita linha base do feixe. |
Caso 3: feixe "impróprio" constituído de todas as retas do plano paralelas
entre si no mesmo sentido. |
|
|
|
|
|
Propriedades:
-
Duas retas de um feixe o determinam
univocamente.
-
Dado um feixe de retas, por cada ponto do
plano (exceto o caso no qual o ponto seja o centro do feixe do
caso 1), passa uma e só uma reta do feixe.
A partir das três situações, podemos definir
respectivamente três lugares geométricos:
|
|
DH 09 - Circunferência que é o lugar geométrico
dos pontos eqüidistantes do centro do feixe (que coincide com o
centro da circunferência) . Ex. circunferência de centro P e raio
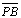 . . |
DH 10 - Hipercírculo ou curva eqüidistante,
que é o lugar geométrico dos pontos eqüidistantes a linha base do feixe
(reta a),
que estão do mesmo lado em relação à ela. Ex. o arco A'B'C' é um
hipercírculo e apresenta como linha
base a reta a. As retas do feixe (m,n, d,c) denominam-se raios e
são perpendiculares à linha base. |
DH 11 - Horocírculo ou curva limitante, que
é o lugar geométrico dos pontos eqüidistantes do ponto ideal (H). Ex.
o arco KLM é um
horocírculo com vértice em H. As retas dos feixes denominam-se raios
e são perpendiculares à
curva limitante. |
|
|
|
|
Finalmente podemos afirmar que por três pontos não
alinhados do plano passa uma e só uma circunferência, ou hipercírculo ou
horocírculo.
|
Analise a seguinte situação:
qual a relação do quadrilátero de Saccheri com uma das curvas dadas? |
Resposta |
Após a atividade 11, o Resumo foi atualizado.
 |
Resumo da Geometria
Hiperbólica (RGH) |
|
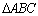 de lados
de lados
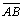 ,
,
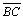 e
e
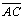 e
pontos médios respectivamente M, N, L.
e
pontos médios respectivamente M, N, L. 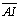 e
e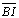
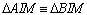 , pois
, pois
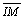 é comum,
é comum,
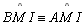 (retos) e
(retos) e
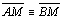 (M é ponto
médio de
(M é ponto
médio de 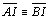
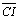
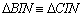 , pois
, pois
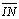 é comum,
é comum,
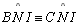 (retos) e
(retos) e
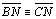
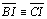
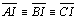 , ou seja I é
eqüidistante dos vértices do triângulo.
, ou seja I é
eqüidistante dos vértices do triângulo.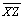
 , pois
, pois
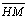 é comum,
é comum,
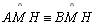 (retos) e
(retos) e
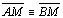 (M é ponto
médio de
(M é ponto
médio de 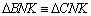 ,
pois
,
pois 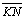 é comum,
é comum,
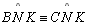 (retos) e
(retos) e
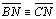 (N é ponto
médio de
(N é ponto
médio de 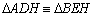 ,
pois
,
pois 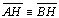 (por
05.5),
(por
05.5), 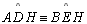 (retos)
e
(retos)
e 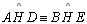 (por 05.5 e
(por 05.5 e
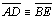
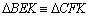 , pois
, pois
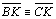 (por 05.6),
(por 05.6),
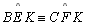 (retos) e
(retos) e
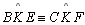 (por 05.6 e
(por 05.6 e
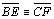
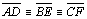 , ou seja, os
vértices do triângulo são eqüidistantes da perpendicular comum
, ou seja, os
vértices do triângulo são eqüidistantes da perpendicular comum
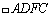 é um
quadrilátero de Saccheri, de base
é um
quadrilátero de Saccheri, de base
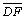 .
.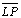 é
perpendicular à
é
perpendicular à 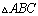 , ou seja
, ou seja
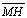 ,
,
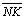 e
e
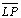 , são
perpendiculares à reta
, são
perpendiculares à reta
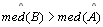 e
e
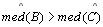 . (Devemos
provar o
mesmo se considerarmos as demais situações). Tracemos D e E em
. (Devemos
provar o
mesmo se considerarmos as demais situações). Tracemos D e E em
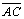 , tais que
, tais que
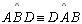 e
e
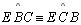
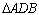 e
e
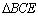 são isósceles,
com
são isósceles,
com 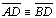 e
e 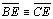 .
.
 .
.