 |
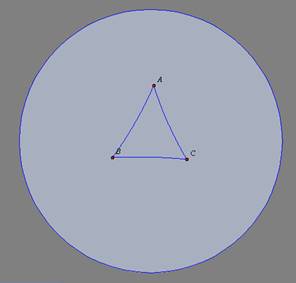
Definição
Hiperbólica 12: A deficiência (defeito ou diferença) de um
triângulo qualquer
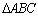 é a diferença entre 180o e a soma das medidas dos seus
ângulos internos.
é a diferença entre 180o e a soma das medidas dos seus
ângulos internos.
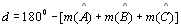
|
Note que a deficiência de um triângulo euclidiano é igual
a zero.
| No do
Passo |
Passo |
Justificativa |
| 01 |
|
Hipótese |
|
02 |
A soma das
deficiências dos triângulos
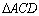 e
e
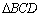 é dada por:
é dada por:
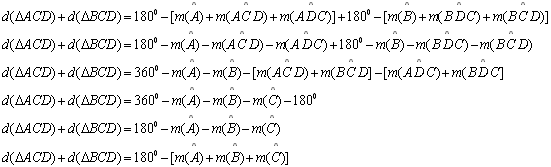
|
DH 12 |
| 03 |
A
deficiência do triângulo
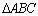 é
é
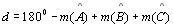 |
DH 12 |
| 04 |
Portanto A
soma das deficiências dos triângulos
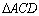 e
e
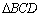 é igual a deficiência de
é igual a deficiência de
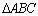 . . |
02; 03 |
Podemos estender o conceito de deficiência para os outros
polígonos. Assim a deficiência de um quadrilátero
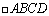 é é
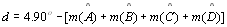 . .
Generalizando, a deficiência de qualquer região poligonal
de n lados é dada por:
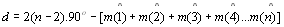
No estudo de áreas, vamos nos limitar a análise de áreas
de regiões poligonais. Na Geometria Euclidiana podemos afirmar que:
-
A área A é uma função unívoca do conjunto P de todas
as regiões poligonais no conjunto R dos números reais.
-
A área de uma região poligonal P é sempre positiva,
ou seja, para todo P, A(P)>0.
-
Se dois triângulos são congruentes, então eles
apresentam a mesma área.
-
Se duas regiões poligonais P1 e P2 adjacentes (ou
contíguas), isto é, polígonos que apresentam em comum somente pontos de
seu contorno, então a reunião das duas regiões terá a soma das áreas de
P1 e P2, ou seja, A(P1 U P2) = A(P1) + A(P2).
Na Geometria Hiperbólica, se considerarmos a deficiência
de um triângulo (ou de um polígono qualquer) como um número
real, podemos definir uma função onde a cada região poligonal P associa um
número real d(P). Note que as afirmações 1 a 4 também valem também para essa
função.
Podemos ainda definir a função área de uma região
poligonal em relação a sua deficiência. Dado um triângulo qualquer
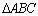 , definimos uma constante k, tal que , definimos uma constante k, tal que
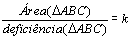 , ou seja, , ou seja,
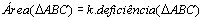 . .
OBS.: "È impossível conhecer o efetivo
valor de k. Há infinitas geometrias concebíveis, cada uma com um valor
diferente de k (01)".
Uma vez que a soma dos ângulos de um triângulo
hiperbólico é sempre positiva e menor que 180o, sabemos que a
deficiência do
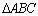 ,
dada por ,
dada por
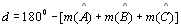 ,
é sempre positiva e menor que 180o. ,
é sempre positiva e menor que 180o.
Na fórmula
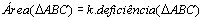 sabemos que
o segundo membro é menor que sabemos que
o segundo membro é menor que
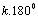 .
Podemos afirmar então que .
Podemos afirmar então que
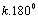 é o limite superior para as áreas dos triângulos hiperbólicos.
é o limite superior para as áreas dos triângulos hiperbólicos.
|
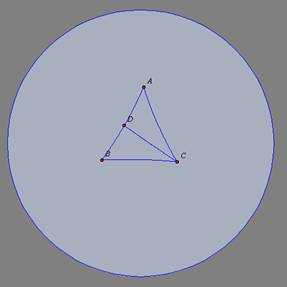
Analise a seguinte situação:
na geometria euclidiana há uma relação entre a medida da diagonal de uma
quadrado com a medida de seu lado, que é o número irracional
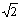 . Explore
dinamicamente a figura e verifique se, na geometria hiperbólica, essa
relação é mantida. A que valores essa relação tende quando o lado do
quadrado aumenta e quando ele torna-se bem pequeno. . Explore
dinamicamente a figura e verifique se, na geometria hiperbólica, essa
relação é mantida. A que valores essa relação tende quando o lado do
quadrado aumenta e quando ele torna-se bem pequeno. |
Resposta |
|
|
|
Após a atividade 12, o Resumo foi atualizado.
 |
Resumo da Geometria
Hiperbólica (RGH) |
|

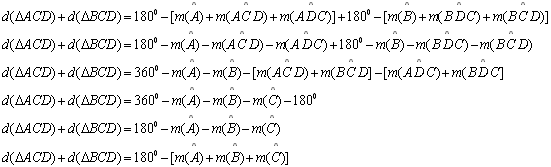
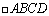 é
é
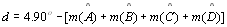 .
. 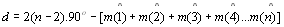
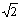 . Explore
dinamicamente a figura e verifique se, na geometria hiperbólica, essa
relação é mantida. A que valores essa relação tende quando o lado do
quadrado aumenta e quando ele torna-se bem pequeno.
. Explore
dinamicamente a figura e verifique se, na geometria hiperbólica, essa
relação é mantida. A que valores essa relação tende quando o lado do
quadrado aumenta e quando ele torna-se bem pequeno.