Termos Primitivos
Ponto
Reta
Plano
Relações Primitivas (que relacionam os termos primitivos)
Estar em
Entre
Congruência
Axiomas de Incidência
Para cada dois pontos A, B há sempre uma reta a que está associada com cada um dos dois pontos A, B.
Para dois pontos A, B não há mais do que uma reta que está associada com cada um dos dois pontos A, B.
Sobre uma reta há sempre, pelo menos, dois pontos. Há pelo menos três pontos que não estão sobre uma mesma reta.
Axiomas de Ordem
Se um ponto B está entre um ponto A e um ponto C, então A, B, C são três pontos distintos duma reta,e B está também entre C e A. Em símbolos: A * B * C ou C * B * A.
Para cada dois pontos A e C há sempre, pelo menos, um ponto B sobre a reta AC tal que C está entre A e B. Em símbolos: A * C * B.
Dados três pontos quaisquer duma reta, não há mais do que um que está entre os outros dois.
(Axioma de Pasch) Toda reta traçada de um ponto do triângulo a um seu ponto interno intersectará o triângulo, se prolongada, em mais um ponto.
Axiomas de Congruência
Se A e B são dois pontos de uma reta a e A' é um ponto de uma reta a', pode-se sempre encontrar sobre uma semi-reta de a' um ponto B' determinado por A' tal que o segmento AB seja congruente ou igual ao segmento A'B'. Em símbolos: AB ≡ A'B'
(transitividade) Se os segmentos A'B' e A''B'' são congruentes com o mesmo segmento AB, também o segmento A'B' é congruente com o segmento A''B''.
Sejam AB e BC dois segmentos da reta a sem pontos comuns, e por outro lado A'B' e B'C' dois segmentos sem pontos comuns sobre a mesma reta a ou sobre outra distinta a': se AB ≡ A'B' e BC ≡ B'C' então AC ≡ A'C'.
Sejam
dados um ângulo
![]() ,
uma reta a' e um dos lados determinados por a', e representemos por h'
uma semi-reta de a' que parte de O': existe então uma e uma só semi-reta
k' tal que o ângulo
,
uma reta a' e um dos lados determinados por a', e representemos por h'
uma semi-reta de a' que parte de O': existe então uma e uma só semi-reta
k' tal que o ângulo
![]() seja congruente ou igual ao ângulo
seja congruente ou igual ao ângulo
![]() ;
utilizando símbolos:
;
utilizando símbolos:
![]() e
tal que por sua vez todos os pontos interiores do ângulo
e
tal que por sua vez todos os pontos interiores do ângulo
![]() estão
situados no lado dado em relação a a'. Todo ângulo é congruente consigo
mesmo, isto é, verifica-se sempre
estão
situados no lado dado em relação a a'. Todo ângulo é congruente consigo
mesmo, isto é, verifica-se sempre
![]() .
.
Se em dois
triângulos ABC e A'B'C' se verificam as congruências AB ≡ A'B', AC ≡
A'C',
![]() ,
então tem-se sempre também que
,
então tem-se sempre também que
 .
.
(Axioma de Arquimedes): Se AB e CD são segmentos quaisquer, então existe um número natural n tal que n segmentos congruentes a CD construídos continuamente a partir de A sobre a semi-reta AB, conterá o ponto B.
(Axioma da Continuidade Circular): Se uma circunferência C tem um ponto no interior e um ponto no exterior de uma outra circunferência C, então as duas circunferências se cortam em dois pontos.
(Axioma da Continuidade Elementar): Se uma extremidade de um segmento de reta está no interior de uma circunferência e a outra extremidade no exterior, então o segmento corta a circunferência em um ponto.
Os pontos que estão situados entre A e B chamam-se os pontos do segmento AB ou BA.
Toda a reta é dividida por qualquer dos seus pontos em duas semi-retas.
A duas
semi-retas h e k que partem de um ponto A e que não formam uma reta,
damos o nome de ângulo e o designamos por
![]() ou
ou
![]()
Dadas duas
semi-retas h e k, os pontos do plano que em relação a h estão no mesmo
lado que k, e ao mesmo tempo estão no mesmo lado que h em relação a k
denominam-se pontos interiores do ângulo
![]() e formam o espaço angular [interior] deste ângulo.
e formam o espaço angular [interior] deste ângulo.
Um sistema de segmentos AB, BC, CD,...KL chama-se uma poligonal que une os pontos A e L; esta poligonal também se designará abreviadamente por ABCD...KL. Os pontos do interior dos segmentos AB, BC, CD,...,KL, assim como os pontos A,B,C,D,...K,L chamam-se, todos eles os pontos da poligonal. Em particular, se os pontos A,B,C,D,...,K,L estão todos num plano e se, além disso, o ponto L coincide com o ponto A, então a poligonal chamar-se-á um polígono e designar-se-á por polígono ABCD...K. Os segmentos AB, BC, CD,...,KL chamam-se também os lados do polígono. Os pontos A,B,C,D,...K chamam-se os vértices do polígono. Polígonos com 3, 4, ..., n vértices chamam-se triângulos, quadriláteros, ..., polígonos com n vértices [ou n-ágonos].
Dois ângulos que têm o vértice e um lado comuns e cujos lados não comuns constituem uma reta, chamam-se ângulos adjacentes suplementares. Dois ângulos com o vértice comum em que cada lado dum deles constitui com um dos lados do outro uma reta, chamam-se ângulos verticalmente opostos. Um ângulo que é congruente com um seu ângulo adjacente suplementar, chama-se um ângulo reto.
Um triângulo ABC diz-se congruente com um triângulo A'B'C', se são verificadas todas as congruências:
![]() ,
,![]() ,
,![]() ,
,
![]() ,
,
![]() e
e
![]() .
.
Um ângulo que é maior que o seu ângulo adjacente suplementar, ou maior do que um ângulo reto, chama-se um ângulo obtuso; um ângulo que é menor do que o seu ângulo adjacente suplementar, ou do que um ângulo reto, chama-se um ângulo agudo.
Os ângulos
![]() ,
,
![]() e
e
![]() que pertencem a um triângulo ABC chamam-se os ângulos deste
triângulo; os ângulos adjacentes suplementares chamam-se os seus
ângulos externos.
que pertencem a um triângulo ABC chamam-se os ângulos deste
triângulo; os ângulos adjacentes suplementares chamam-se os seus
ângulos externos.
Duas retas dizem-se paralelas se estão num mesmo plano e não se intersectam.
Se M e um ponto qualquer dum plano a, então ao conjunto de todos aqueles pontos A, em a, para os quais os segmentos MA são congruentes entre si, chama-se circunferência; a M chama-se centro da circunferência e MA é dito raio.
Um ponto está no interior ou no exterior de uma circunferência se o segmento de reta que une ao centro da circunferência é respectivamente menor ou maior do que o raio. No caso de ser igual ao raio, dizemos que o ponto em questão pertence a circunferência.
Duas retas dizem-se perpendiculares se são concorrentes e formam ângulos adjacentes suplementares congruentes.
Bissetriz interna de um triângulo é o segmento, com extremidades num vértice e no lado oposto, que divide o ângulo desse vertíce em dois ângulos congruentes.
Mediana de um triângulo é um segmento com extremidades num vértice e no ponto médio do lado oposto.
Os triângulos, quanto aos lados se classificam em:
equilátero : seus três lados são congruentes;
isósceles: dois de seus lados são congruentes, e o outro lado é dito 'base';
escaleno: nenhum de seus lados são congruentes.
Círculo é a região compreendida por uma circunferência e sua região interior.
Chama-se arco de circunferência, a região da circunferência limitada por dois de seus pontos.
Ângulo Central relativo a uma circunferência é o ângulo que apresenta o vértice no centro da circunferência.
Ângulo Inscrito relativo a uma circunferência é um ângulo que apresenta o vértice na circunferência e os lados são secantes a ela.
Diz-se que um polígono está inscrito numa circunferência quando todos os seus vértices são pontos dessa circunferência.
Dois ângulos são complementares se, e somente se, a soma de suas medidas for igual a um ângulo reto.
Num triângulo isósceles a mediatriz, a bissetriz e a altura relativas à base são coincidentes.
Corda de um circunferência é um segmento cujas extremidades são pontos da circunferência
Teoremas demonstrados sem o Postulado das Paralelas
(LAL)
Dados os triângulos ABC e A'B'C' se
![]() ,
,
![]() e
e
![]() ,
então os triângulos são congruentes.
,
então os triângulos são congruentes.
Por um ponto qualquer de uma reta existe uma única reta perpendicular à ela.
Se uma reta é levantada sobre uma outra reta, formará com ela ou dois ângulos retos ou ângulos cuja soma é igual a dois retos.
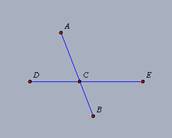 |
Se por um
ponto C de uma reta
|
Se uma reta intersecta outras duas formando com ela ângulos alternos internos iguais entre si, as duas retas são paralelas.
Se uma reta d intersecta outras duas a, b, formando um ângulo externo congruente ao interno oposto da mesma parte, ou também os dois internos da mesma parte iguais a dois retos, então a e b são paralelas.
Um ângulo externo de um triângulo é maior que qualquer um dos ângulos internos não adjacentes.
Se a soma das medidas de dois ângulos adjacentes é 180o, então os lados são alinhados.
(LLL)
Dados os triângulos ABC e A'B'C' se
![]() ,
,
![]() e
e
![]() ,
então os triângulos são congruentes.
,
então os triângulos são congruentes.
(ALA)
Dados os triângulos ABC e A'B'C' se
![]() ,
,
![]() e
e
![]() ,
então os triângulos são congruentes.
,
então os triângulos são congruentes.
|
Dado um triângulo ABC, tracemos a reta que passa
pelos pontos médios de dois de seus lados
|
A soma de dois quaisquer ângulos de um triângulo é menor que 180o.
Os ângulos da base de um triângulo isósceles são congruentes.
(LAAo)
Dados os triângulos ABC e A'B'C' se
![]() ,
,
![]() e
e
![]() ,
então os triângulos são congruentes.
,
então os triângulos são congruentes.
Para cada dois pontos A e C há sempre pelo menos um ponto D sobre a reta AC, que está entre A e C.
Propriedades
Igualdades e desigualdades entre grandezas geométricas do mesmo tipo obedecem as mesmas leis das equações e inequações entre números naturais. Sejam a, b, c e d grandezas quaisquer homogêneas, temos:
P 01:Se a = b e c = b, então a = c
P 02:Se a = b e c = d, então a + c = b + d
P 03:Se a = b e c = d, então a - c = b - d
P 04:a +b > a
P 05:Se a = b e c > d, então a + c > b + d
P 06:Se a > b e b = c, então a > c
P 07:Se a < b e c = a, então c < b
P 08: Se a = b, então a + c = b + c
P 09: Se a não é menor que b, e a é diferente de b, então a > b
P 10: Se a > b e c = b, então c < a
P 11: Se a = b e c = d; então a + c = b + d
P 12: Se a < b e c = d; então a + c < b + d
P 13: Se a < b e a + b = c; então a + a < a + b => 2a < c => a < c / 2
P 14: Se a = b e b < c; então a < c
P 15: Se a > b e b > c; então a > c
P 16: Se a > b e c > d; então a + c > b + d
P 17: Se a < b e c + a = 2b; então c > b
P 18: Se a < b e c > b; então a < c
P 19: Se a < b e c < b; então a + c < 2b
P 20: Se a = b e a < c; então b < c
P 21: Se a + b = c e d + e = c ; então a + b + d + e = 2c
P 22: Se a = b e a + c = d ; então b + c = d
P 23: Se a + a + b + b = 2a + 2b = c ; então a + b = c / 2
P 24: Se a > b e c = b / 2 ; então a > 2c ou ainda c < a / 2
P 25: Se a + b = c + d e b = d, então a = c
Axiomas da geometria hiperbólica
(Axioma das retas secantes e não secantes) Seja b uma reta qualquer e A um ponto não situado sobre ela. Existem sempre duas semi-retas a1 e a2 que partem de A e não constituem uma só reta e que não cortam b, mas toda a semi-reta que parte de A e situada no espaço angular formado por a1, a2 corta a reta b.
Definições da geometria hiperbólica
Supondo a
reta b dividida por um qualquer dos seus pontos B em duas semi-retas b1
e b2, e estando as semi-retas a1 e b1
de um lado da reta
![]() e a2, b2 do outro lado da mesma reta, dizemos que
a semi-reta a1 é paralela à semi-reta b1, e
analogamente a semi-reta a2 é paralela a b2.Dizemos
que as duas semi-retas a1, a2 são paralelas à reta b.
e a2, b2 do outro lado da mesma reta, dizemos que
a semi-reta a1 é paralela à semi-reta b1, e
analogamente a semi-reta a2 é paralela a b2.Dizemos
que as duas semi-retas a1, a2 são paralelas à reta b.
Toda a semi-reta determina um sentido: dizemos que todas as semi-retas paralelas entre si determinam um mesmo sentido. Uma semi-reta que parte de A com o sentido a será designada em gera por (A,a).Uma reta tem sempre dois sentidos. Em geral uma reta cujos sentidos são a e b é designada por (a,b).
|
As retas b e c são chamadas assintóticas (ou a-paralelas)
por P em relação a reta a. As retas que passam por P e por um ponto
situado no interior de
|
As retas b e c são paralelas assintóticas a a por P. A perpendicular a a por P forma com as retas b e c ângulos denominados "Ângulos de Paralelismo".
Teoremas da geometria hiperbólica
Seja a uma reta qualquer e P um ponto não situado sobre ela. Pelo ponto
P passam as retas b e c, paralelas a a por P. Toda reta d que passa por
P, e por um ponto qualquer O, situado no espaço angular formado por
![]() ,
é paralela à reta a.
,
é paralela à reta a.
Dada uma reta a e um ponto P fora dela, existe para cada sentido uma única reta assintótica em relação à reta a por P.
As paralelas assintóticas b e c em relação à reta a por P formam ângulos de paralelismo congruentes e agudos .
 ,
traçarmos outras duas retas
,
traçarmos outras duas retas
 e ainda se
e ainda se