|
Impulsionados pela característica “estranha” do V postulado alguns matemáticos iniciaram estudos sobre a possibilidade de demonstrar que também o V postulado seria na realidade um teorema. A intenção inicial era, mantendo os termos primitivos, os termos definidos (com exceção da definição 23 de “paralelas” e incluindo uma definição própria), os axiomas e os postulados (com exceção do quinto) criar uma nova axiomática onde fosse possível demonstrar um novo teorema (com o mesmo teor do quinto postulado de Euclides). Todos os teoremas de Euclides que não utilizam o quinto postulado em suas provas também seriam aceitos. Apresentamos somente a proposta de Poseidonios (c. 135 a.C – metade do séc. I), e a seguir relacionamos as principais proposições dos matemáticos (Quadro 1.2) na tentativa de provar o quinto postulado. Em todas elas foram identificadas implicitamente alguma contradição lógica ou afirmações que não podem ser assumidas pelas noções comuns, definições, axiomas e teoremas demonstrados em precedência.
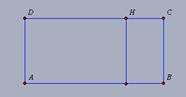
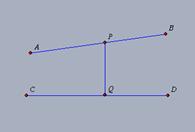
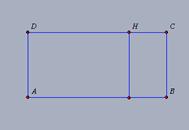
Conhecemos o trabalho de Poseidonios pelos textos de Proclus (410-485). Ele propôs uma nova definição para retas paralelas, utilizando a propriedade de eqüidistância e considerou que a sua definição e a dada por Euclides fossem equivalentes. Dessa forma, seria possível assumir os demais teoremas dos Elementos, substituindo a referência ao postulado V (de Euclides) por um seu teorema demonstrado a partir de sua definição de retas paralelas. DEFINIÇÃO: Diz-se paralelas as retas que estejam no mesmo plano e que, se prolongadas indefinidamente em ambas as direções, mantenham a mesma distância entre si. Lembramos que a definição de retas paralelas dada por Euclides é: linhas retas paralelas são linhas retas que, estando na mesma superfície plana e sendo estendidas indefinidamente em ambas as direções não chegam a se tocar. No “Comentário al livro I de Euclides”, Proclus desenvolve críticas sobre a equivalência entre as definições de Euclides e de Poseidonios. Ele argumenta apresentando uma hipérbole que se aproxima de suas assíntotas, sem nunca encontrá-las. Essas retas, que são paralelas pela definição de Euclides (se prolongadas indefinidamente não se encontram), não o são pela definição dada por Poseidonios (não são eqüidistantes). Segue o Quadro II, inspirado no levantamento apresentado por TRUDEAU (2004, p.145-146, tradução nossa do original em italiano), dos mais significativos enunciados propostos em substituição ao V postulado, escritos nos termos atuais.
Depois de várias tentativas frustradas em que, substituir o V postulado por qualquer dos listados acima, resultava sempre na geometria euclidiana, os matemáticos passaram a suspeitar que não fosse possível transformar o V postulado em teorema. “Agora é compreensível a frustração de Gauss e dos que sustentavam o ponto de vista lógico: não havia modo de demonstrar o quinto postulado sem introduzir outro, mas todos os postulados levantados (possíveis de substituí-lo), mesmo sendo intuitivamente evidentes, eram destinados a serem ineficazes porque, também se psicologicamente preferíeis, seriam equivalentes ao quinto postulado, e então dele indistinguíveis do ponto de vista essencial, o lógico.” (TRUDEAU, 2004, p. 148, tradução nossa do original em italiano). Ressaltamos o trabalho de Girolamo Saccheri (1667-1733) que, na tentativa de provar que o V postulado derivava dos outros, apresentou um raciocínio no qual “assumindo como hipótese a falsidade da proposição que se pretende demonstrar, chega-se a concluir que ela é falsa. (BONOLA, 1923, p.20)
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||