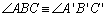|
O objetivo de minha obra é
estabelecer de uma vez por todas a certeza dos métodos matemáticos. David
Hilbert
 |
Após sofrer
pesadas críticas com o amadurecimento do rigor matemático, no séc.
XIX, destacamos a obra Fundamentos da Geometria, publicada em 1899
por David Hilbert (1862-1943), que reescreveu a axiomática de
Euclides, reorganizando e elaborando uma rigorosa apresentação
lógico-dedutiva dessa geometria.
Hilbert considerou como termos
primitivos os conceitos (objetos) de ponto, reta e plano e supôs
três relações entre tais conceitos (objetos): “estar situação”
(incidir); “entre” e “congruente”. Em seguida classificou seus
axiomas nos grupos: incidência, ordem, congruência, continuidade e
paralelismo, cobrindo as lacunas encontradas na obra Euclides. |
|
Hilbert |
Utilizamos a axiomática
de Hilbert, para a justificação das demonstrações apresentadas em nossa
seqüência didática. Inspirados em HILBERT (2003), TERDIMAN (1989) e LINS
(2002), apresentamos no Quadro III a axiomática relativa à geometria plana,
que particularmente é de nosso interesse. Os Termos Definidos TD 01 até TD 11 constam em
HILBERT (2003) e acrescentamos os termos seguintes por serem necessários às
demonstrações propostas em nossas atividades.
Não mais rigor de quanto seja
necessário. Robert L.
Moore
| |
|
AXIOMÁTICA DE HILBERT |
|
TERMOS PRIMITIVOS |
|
TP 01 |
Ponto |
|
TP 02 |
Reta |
|
TP 03 |
Plano |
|
RELAÇÕES PRIMITIVAS |
|
RP 01 |
Estar em |
|
RP 02 |
Entre |
|
RP 03 |
Congruente |
|
AXIOMAS DE INCIDÊNCIA |
|
I 01 |
Para cada dois pontos A, B há sempre uma reta a que está
associada com cada um dos dois pontos A, B. |
|
I 02 |
Para dois pontos A, B não há mais do que uma reta que está
associada com cada um dos dois pontos A, B. |
|
I 03 |
Sobre uma reta há sempre, pelo menos, dois pontos. Há pelo
menos três pontos que não estão sobre uma mesma reta. |
|
AXIOMAS DE ORDEM |
|
O 01 |
Se um ponto B está entre um ponto A e um ponto C, então A,
B, C são três pontos distintos duma reta,e B está também
entre C e A. Em símbolos: A * B * C ou C * B * A. |
|
O 02 |
Para cada dois pontos A e C há sempre, pelo menos, um ponto
B sobre a reta AC tal que C está entre A e B. Em símbolos: A
* C * B. |
|
O 03 |
Dados três pontos quaisquer duma reta, não há mais do que
um que está entre os outros dois. |
|
O 04 |
(Axioma de Pasch) Toda reta traçada de um ponto do
triângulo a um seu ponto interno intersectará o triângulo,
se prolongada, em mais um ponto. |
|
AXIOMAS DE CONGRUÊNCIA |
|
C 01 |
Se A e B são dois pontos de uma reta a e A' é um ponto de
uma reta a', pode-se sempre encontrar sobre uma semi-reta de
a' um ponto B' determinado por A' tal que o segmento AB seja
congruente ou igual ao segmento A'B'. Em símbolos: AB ≡ A'B' |
|
C 02 |
(transitividade) Se os segmentos A'B' e A''B'' são
congruentes com o mesmo segmento AB, também o segmento A'B'
é congruente com o segmento A''B''. |
|
C 03 |
Sejam AB e BC dois segmentos da reta a sem pontos comuns, e
por outro lado A'B' e B'C' dois segmentos sem pontos comuns
sobre a mesma reta a ou sobre outra distinta a': se AB ≡
A'B' e BC ≡ B'C' então AC ≡ A'C'. |
|
C 04 |
Sejam dados um ângulo 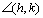 , uma reta a' e
um dos lados determinados por a', e representemos por h' uma
semi-reta de a' que parte de O': existe então uma e uma só
semi-reta k' tal que o ângulo , uma reta a' e
um dos lados determinados por a', e representemos por h' uma
semi-reta de a' que parte de O': existe então uma e uma só
semi-reta k' tal que o ângulo 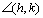 seja congruente
ou igual ao ângulo seja congruente
ou igual ao ângulo 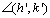 ; utilizando
símbolos: ; utilizando
símbolos: 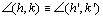 e tal que por sua
vez todos os pontos interiores do ângulo e tal que por sua
vez todos os pontos interiores do ângulo 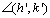 estão situados no
lado dado em relação a a'. Todo ângulo é congruente consigo
mesmo, isto é, verifica-se sempre estão situados no
lado dado em relação a a'. Todo ângulo é congruente consigo
mesmo, isto é, verifica-se sempre 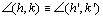 . . |
|
C 05 |
Se em dois triângulos ABC e A'B'C' se verificam as
congruências AB ≡ A'B', AC ≡ A'C', 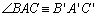 , então tem-se
sempre também que , então tem-se
sempre também que
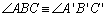 |
|
AXIOMAS DE CONTINUIDADE |
|
Ct 01 |
(Axioma de Arquimedes): Se AB e CD são segmentos quaisquer,
então existe um número natural n tal que n segmentos
congruentes a CD construídos continuamente a partir de A
sobre a semi-reta AB, conterá o ponto B. |
|
Ct 02 |
(Axioma da Continuidade Circular): Se uma circunferência C
tem um ponto no interior e um ponto no exterior de uma outra
circunferência C, então as duas circunferências se cortam em
dois pontos. |
|
Ct 03 |
(Axioma da Continuidade Elementar): Se uma extremidade de
um segmento de reta está no interior de uma circunferência e
a outra extremidade no exterior, então o segmento corta a
circunferência em um ponto. |
|
AXIOMAS DE PARALELISMO |
|
P 01 |
Seja a uma reta qualquer e A um ponto exterior a a; então,
no plano determinado por a e A há, no máximo, uma reta que
passa por A e não corta a. |
|
TERMOS DEFINIDOS |
|
D 01 |
Os pontos que estão situados entre A e B chamam-se os
pontos do segmento AB ou BA. |
|
D 02 |
Toda a reta é dividida por qualquer dos seus pontos em duas
semi-retas. |
|
D 03 |
A duas semi-retas h e k que partem de um ponto A e que não
formam uma reta, damos o nome de ângulo e o
designamos por 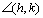 ou ou 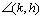 |
|
D 04 |
Dadas duas semi-retas h e k, os pontos do plano que em
relação a h estão no mesmo lado que k, e ao mesmo tempo
estão no mesmo lado que h em relação a k denominam-se pontos
interiores do ângulo 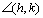 e formam o
espaço angular [interior] deste ângulo. e formam o
espaço angular [interior] deste ângulo. |
|
D 05 |
Um sistema de segmentos AB, BC, CD,...KL chama-se uma
poligonal que une os pontos A e L; esta poligonal também
se designará abreviadamente por ABCD...KL. Os pontos do
interior dos segmentos AB, BC, CD,...,KL, assim como os
pontos A,B,C,D,...K,L chamam-se, todos eles os pontos da
poligonal. Em particular, se os pontos A,B,C,D,...,K,L
estão todos num plano e se, além disso, o ponto L coincide
com o ponto A, então a poligonal chamar-se-á um polígono
e designar-se-á por polígono ABCD...K. Os segmentos AB, BC,
CD,...,KL chamam-se também os lados do polígono. Os
pontos A,B,C,D,...K chamam-se os vértices do polígono.
Polígonos com 3, 4, ..., n vértices chamam-se triângulos,
quadriláteros, ..., polígonos com n vértices [ou
n-ágonos]. |
|
D 06 |
Dois ângulos que têm o vértice e um lado comuns e cujos
lados não comuns constituem uma reta, chamam-se ângulos
adjacentes suplementares. Dois ângulos com o vértice
comum em que cada lado dum deles constitui com um dos lados
do outro uma reta, chamam-se ângulos verticalmente
opostos. Um ângulo que é congruente com um seu ângulo
adjacente suplementar, chama-se um ângulo reto. |
|
D 07 |
Um triângulo ABC
diz-se congruente com um triângulo A'B'C', se são
verificadas todas as congruências:
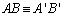 , ,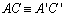 , ,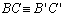 , , 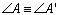 , , 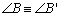 e e 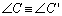 . . |
|
D 08 |
Um ângulo que é maior que o seu ângulo adjacente
suplementar, ou maior do que um ângulo reto, chama-se um
ângulo obtuso; um ângulo que é menor do que o seu ângulo
adjacente suplementar, ou do que um ângulo reto, chama-se um
ângulo agudo. |
|
D 09 |
Os ângulos 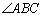 , ,  e e 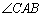 que pertencem a
um triângulo ABC chamam-se os ângulos deste
triângulo; os ângulos adjacentes suplementares chamam-se
os seus ângulos externos. que pertencem a
um triângulo ABC chamam-se os ângulos deste
triângulo; os ângulos adjacentes suplementares chamam-se
os seus ângulos externos. |
|
D 10 |
Duas retas dizem-se paralelas se estão num mesmo
plano e não se intersectam. |
|
D 11 |
Se M e um ponto qualquer dum plano
a,
então ao conjunto de todos aqueles pontos A, em
a, para os quais os segmentos MA são congruentes entre si, chama-se
circunferência; a M chama-se centro da circunferência
e MA é dito raio. |
|
D 12 |
Um ponto está no interior ou no exterior de uma
circunferência se o segmento de reta que une ao centro da
circunferência é respectivamente menor ou maior do que o
raio. No caso de ser igual ao raio, dizemos que o ponto em
questão pertence a circunferência. |
|
D 13 |
Duas retas dizem-se perpendiculares se são
concorrentes e formam ângulos adjacentes suplementares
congruentes. |
|
D 14 |
Bissetriz interna de um triângulo é o segmento, com extremidades num
vértice e no lado oposto, que divide o ângulo desse vértice
em dois ângulos congruentes. |
|
D 15 |
Mediana
de um triângulo é um segmento com extremidades num vértice
e no ponto médio do lado oposto. |
|
D 16 |
Os
triângulos, quanto aos lados se classificam em:
eqüilátero
: seus três lados são congruentes;
isósceles:
dois de seus lados são congruentes, e o outro lado é dito
'base';
escaleno: nenhum de seus lados são congruentes. |
|
D 17 |
Ponto Médio
de um segmento é o ponto desse segmento eqüidistante das
extremidades. |
|
D 18 |
Círculo
é a região compreendida por uma circunferência e sua região
interior. |
|
D 19 |
Chama-se arco de circunferência, a região da
circunferência limitada por dois de seus pontos. |
|
D 20 |
Ângulo Central relativo a uma circunferência é o ângulo que apresenta o
vértice no centro da circunferência. |
|
D 21 |
Ângulo Inscrito relativo a uma circunferência é um ângulo que apresenta o
vértice na circunferência e os lados são secantes a ela. |
|
D 22 |
Diz-se
que um polígono está inscrito numa
circunferência quando todos os seus vértices são pontos
dessa circunferência. |
|
D 23 |
Dois
ângulos são complementares se, e somente se, a soma
de suas medidas for igual a um ângulo reto. |
|
D 24 |
Num
triângulo isósceles a mediatriz, a bissetriz e a
altura relativas à base são coincidentes. |
|
D 25 |
Corda
de um circunferência é um segmento cujas extremidades são
pontos da circunferência |
|
|
|
|
|