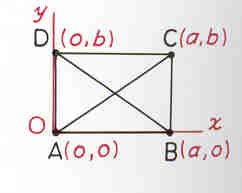
Exemplo de uma aplicação utilizando o conceito de coordenadas


Exemplo 1:

Teorema: As diagonais de um rectângulo têm comprimentos iguais.

Demonstração: Dado um rectângulo ABCD com diagonais [AC] e [DB] ( Figura 1) queremos provar que AC = DB.

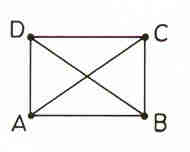
fig7.jpg (2774 bytes)
        Figura 1

Coloquemos um sistema de coordenadas no rectângulo ABCD tal como nos mostra a figura 2. 

fig8.jpg (4574 bytes)
        Figura 2
 

    Pela definição de distância obtemos o seguinte:

AC = [(a – 0)² + (b – 0)²]½ =  (a² + b²)½

DB = [ (a – 0)² + ( 0 – b)²]½ = (a² + b² )½

Portanto concluímos que AC = DB.

 

    Lembremos a noção de distância entre dois pontos arbitrários P(a,b) e Q(c,d). Assim a distância é a raíz quadrada da soma do quadrado de (c – a) com o quadrado de (d – b), ou seja, PQ = [(c – a)² + (d – b)²]½.

Volta ao Índice