Atividade 2: Explorando o Disco de Poincaré

 

Explore dinamicamente as figuras e observe o seu comportamento:

  1. Como são as retas no plano euclidiano? E no plano hiperbólico?

  2. E os segmentos de retas?

  3. E os ângulos? Há divergência nas suas medidas?

Plano Euclidiano (P.E.)

Plano Hiperbólico (P.H.)

Por favor habilite Java para uma construção interativa (com Cinderella).

Por favor habilite Java para uma construção interativa (com Cinderella).

 

Modelo de Poincaré

Podemos definir modelo de um sistema axiomático formal como sendo "toda interpretação dos termos primitivos tais que os axiomas tornam-se enunciados verdadeiros (3)", o que nos fornece uma confirmação de coerência.

Estudaremos o modelo desenvolvido por Poincaré, que é um dos modelos disponíveis no software Cinderella, para o estudo da geometria hiperbólica. O software apresenta também o modelo de Klein, que não fará parte de nosso estudo.

 

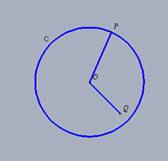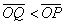Seja C uma circunferência do plano euclidiano de centro O e raio . O interior de C é formado por todos os pontos Q tais que . O interior de C é o plano hiperbólico e a circunferência e chamada de circunferência limite ou horizonte.

 

Nesse sistema os termos primitivos foram interpretados como segue:

Termos Primitivos
Interpretação

Ponto

Ponto Interno à C

Reta

Diâmetro aberto de C ou um arco de circunferência ortogonal à C

Plano

Interior de C
   

Modelo de Poincaré:

Por favor habilite Java para uma construção interativa (com Cinderella).

Horizonte: circunferência de centro O

Plano: interior da circunferência

Pontos do Modelo: O, A (do interior da circunferência.

Retas: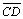 (excluindo as extremidades) e o arco de circunferência arco menor (DE) ortogonal(01) ao horizonte (excluindo as extremidades)

 
   

Inversão

Transformação Geométrica: Inversão
   

Após a definição e construção do modelo a partir de uma circunferência euclidiana, apresentado no link Inversão, passaremos a utilizar o modelo do Cinderella.

 

Voltando a situação inicial, movimente o segmento 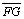até as extremidades pertencerem à circunferência limite. Observe que o arco FG é ortogonal à circunferência limite.  Podemos então apresentar a interpretação dos objetos nas duas geometrias:

Geometria Euclidiana

Geometria Hiperbólica

Termos primitivos

Ponto: são os pontos do plano

Reta: são as retas do plano

Superfície Plana (plano): é o plano euclidiano

 

Ponto: são os pontos internos ao modelo

Reta: são diagonais (euclidianas) ou arcos de círculos (euclidianos) ortogonais à circunferência limite do modelo

Superfície Plana (plano): é o plano de Poincaré

 

Medida de Ângulos

Medida de um ângulo (amplitude) (02): Dado um ângulo qualquer , sua medida será indicada por 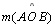e é um número real positivo associado a esse ângulo tal que:

  • Ângulos congruentes têm medidas iguais e, reciprocamente, ângulos que têm medidas iguais são congruentes.

        

  • Se um ângulo é maior que outro, sua medida é maior que a deste outro.

         

  • A um 'ângulo soma ' está associada uma medida que é a soma das medidas dos 'ângulos parcelas'.

         

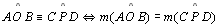
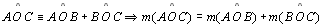
A medida (amplitude) de um ângulo hiperbólico 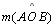coincide com a amplitude euclidiana do ângulo formado pelas retas tangentes aos seus lados.

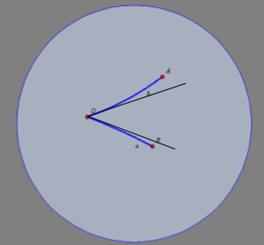
Obs: se o ângulo formado pelas retas tangentes for reto, então AO e BO são ortogonais.
   
Topo   Tela Atividades  

Tela Inicial

 

 

 

 

 

 

 

 

Referências

[01] Diz-se que duas circunferências são ortogonais se o raio de uma, que passa por um dos pontos de intersecção, é tangente à outra circunferência.

[02] DOLCE, Osvaldo; POMPEO, José Nicolau. Fundamentos da Matemática Elementar. Geometria Plana v.9. 7 ed.São Paulo: ed. Atual. 1993.p.26-27

[03] Trudeau, Richard. La revoluzione non euclidea. p. 254. Tradução  nossa do italiano.