|
As atividades anteriores apresentaram o
resumo da geometria absoluta e a apresentação
do modelo de Poincaré. Daremos início ao
aprendizado da geometria hiperbólica apresentando o primeiro axioma.
|
|
Axioma
Hiperbólico 01 (01): Seja b uma reta qualquer e A um ponto não
situado sobre ela. Existem sempre duas semi-retas a1 e a2
que partem de A e não constituem uma só reta e que não cortam b,
mas toda a semi-reta que parte de A e situada no espaço angular formado
por a1, a2 [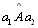 ] corta a reta b
[no ponto B] ] corta a reta b
[no ponto B] |
Definição Hiperbólica 01: Supondo a reta b
dividida por um qualquer dos seus pontos B em duas semi-retas b1
e b2, e estando as semi-retas a1 e b1 de um
lado da reta
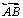 e a2, b2 do outro lado da mesma reta, dizemos que a
semi-reta a1 é paralela à semi-reta b1, e analogamente
a semi-reta a2 é paralela a b2. Dizemos que as duas
semi-retas a1, a2 são paralelas à reta b.
e a2, b2 do outro lado da mesma reta, dizemos que a
semi-reta a1 é paralela à semi-reta b1, e analogamente
a semi-reta a2 é paralela a b2. Dizemos que as duas
semi-retas a1, a2 são paralelas à reta b.
Definição Hiperbólica 02: Toda a semi-reta
determina um sentido: dizemos que todas as semi-retas paralelas entre si
determinam um mesmo sentido. Uma semi-reta que parte de A com o sentido
a
será designada em geral por (A,a).Uma
reta tem sempre dois sentidos. Em geral uma reta cujos sentidos são
a e b
é designada por (a,b).
Podemos definir o sentido do paralelismo: a
semi-reta a2 é paralela a b2 à direita, assim como a
reta a1 é paralela à semi-reta b1 à esquerda. Dizemos
ainda que, por A, passam as paralelas à reta b ( a1, a2
), sendo a1 paralela à esquerda e a2 paralela à
direita.
Observe que pela definição de
retas paralelas as mesmas são retas que
não se intersectam. A definição não afirma que são retas que se mantêm à uma
mesma distância, fato que ocorre na geometria euclidiana. Temos assim que b
e a1 não apresentam pontos em comum, assim como b e a2.
Elas vão se aproximando sem nunca se encontrarem.
|
|
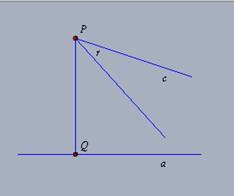
Pelo AH 01 sabemos que as retas b e c
são paralelas à reta a, por A, e também que qualquer reta g que passa por
A e por um ponto do interior do ângulo
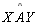 intersecta
a reta a, num ponto B. Vamos investigar como se comportam as retas
de passam por A e por um ponto do interior do ângulo intersecta
a reta a, num ponto B. Vamos investigar como se comportam as retas
de passam por A e por um ponto do interior do ângulo
 . .
Explore dinamicamente a figura. Como se comportam
tais retas d, e, f ?
|
Vamos demonstrar o primeiro teorema hiperbólico.
|
|
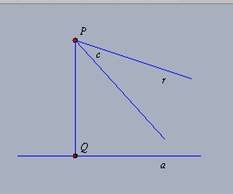
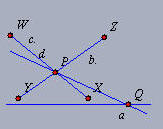
TH 01:
Seja a uma reta qualquer e P um ponto não situado sobre ela. Pelo ponto
P passam as retas b e c, paralelas à reta a. Toda reta d que passa por
P e por um ponto qualquer O, situado no espaço angular formado por XPZ,
conforme figura, é paralela à reta a. |
|
Demonstração |
Hipótese: Dados a reta a, P não situado em a, as retas b e c paralelas
à reta a
por P, e ainda um ponto qualquer O situado no interior
do ângulo 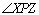 , que
determina com P a reta d, conforme a figura. , que
determina com P a reta d, conforme a figura. |
|
Tese:
d║a |
|
No
do Passo |
Passo |
Justificativa |
|
01 |
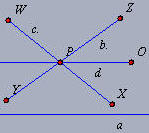 |
As retas b e c são paralelas à reta a pelo ponto
P, e d passa por P e pelo ponto O situado no interior de
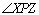 |
|
Hipótese |
|
02 |
A reta d não é paralela à reta a |
Negação da
Tese |
|
03 |
 |
d intersecta a pelo ponto qualquer Q |
|
02,
D 10;
Ct 01 |
|
04 |
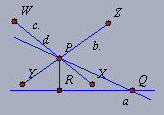 |
Tracemos a perpendicular à reta a por P e chamemos de
R o ponto de intersecção entre a reta a e a perpendicular traçada |
|
T 02, construção |
|
05 |
|
O 04 |
|
06 |
Mas
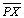 (reta
c) não intersecta a reta a (reta
c) não intersecta a reta a |
Hipótese
(c é paralela a a) |
|
07 |
Contradição. Portanto d║a |
05 e 06 |
Pudemos verificar que há dois tipos de paralelas:
-
as duas paralelas à reta a, pelo ponto P (b e c)
-
as infinitas paralelas (d) que passam por P e por um ponto
qualquer (O)
no interior do ângulo
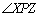 . .
A diferença entre elas é que as retas b e c são retas
limites, ou seja, elas "separam" as retas secantes (que se encontram no
interior de
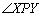 )
das paralelas (que se encontram no interior do
ângulo )
das paralelas (que se encontram no interior do
ângulo
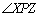 ). ).
Definição Hiperbólica 03: As
retas b e c são chamadas assintóticas (limites ou a-paralelas) por P em relação a
reta a. As retas que passam por P e por um ponto situado no interior de
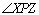 são chamadas paralelas divergentes (ou d-paralelas) por P em relação à reta
a. As retas que passam por P e por um ponto situado no interior de
são chamadas paralelas divergentes (ou d-paralelas) por P em relação à reta
a. As retas que passam por P e por um ponto situado no interior de
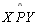 são secantes à reta a. Dizemos que as paralelas assintóticas apresentam um
ponto de convergência, chamado de Ponto Ideal (que não pertence ao
plano hiperbólico).
são secantes à reta a. Dizemos que as paralelas assintóticas apresentam um
ponto de convergência, chamado de Ponto Ideal (que não pertence ao
plano hiperbólico).
O conceito de ponto ideal será utilizado no estudo
de alguns triângulos.
|
|
reta b :
paralela assintótica ou a-paralela à esquerda em relação à reta a, por P |
|
reta c:
paralela assintótica ou a-paralela à direita em relação à reta a, por P |
|
reta d:
uma das infinitas retas paralelas, ditas paralelas divergentes em
relação à reta a, por P |
A seguir vamos demonstrar que as paralelas assintóticas
são únicas.
|
|
TH 02: Dada uma reta a e um ponto
P fora dela, existe para cada sentido uma única reta assintótica em
relação à reta a por P.
|
|
Demonstração |
Hipótese: Dados a reta a, o ponto P não situado em a, e as paralelas assintóticas,
b e c, respectivamente à esquerda e à direita da reta a por P |
|
Tese:
as paralelas assintóticas são únicas em cada sentido (b à esquerda e c à
direita) |
|
No
do Passo |
Passo |
Justificativa |
|
01 |
Dados a reta a,
o ponto P não situado em a e as paralelas assintóticas, b e c,
respectivamene à esquerda
e à direita da reta a por P. |
Hipótese |
|
02 |
Vamos
supor que existe, além de c, uma outra paralela r assintótica à reta a por P,
à direita. |
Negação da
Tese |
|
03 |
Traçando
uma perpendicular à reta a por P, e denominando sua intersecção com a de
Q, temos uma das seguintes situações:
|
02,
T 02; construção |
|
04 |
No caso 1,
a reta r encontraria a, pois r seria uma reta secante à reta a (r se
encontra "abaixo" da paralela limite c).
No caso
2, a reta c encontraria a, pois c seria uma reta secante à reta a (c se
encontra "abaixo" da paralela limite r) |
DH 03 |
|
05 |
Contradição. Logo a reta c é única. |
02 e 04
|
|
06 |
O mesmo pode ser provado para o outro sentido (à
esquerda). Logo a reta c é única. |
02-05 |
|
Analise a seguinte situação:
na geometria euclidiana se duas retas são paralelas a uma terceira, elas
são paralelas entre si. Na geometria hiperbólica, por P temos que b é
paralela assintótica à esquerda à reta a e c é paralela assintótica à direita
à reta a. As retas b e c são paralelas? Justifique sua resposta. |
Resposta |
A partir da atividade 3, podemos atualizar o Resumo da
Geometria Hiperbólica (RGH) com os axiomas, definições e teoremas
hiperbólicos. Tomaremos todos os itens da geometria absoluta e
acrescentaremos os novos itens estudados, que poderão ser utilizados nas
próximas demonstrações.
|
 |
Resumo da Geometria
Hiperbólica (RGH) |
|
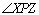 , que
determina com P a reta d, conforme a figura.
, que
determina com P a reta d, conforme a figura.


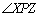 .
.
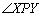 )
das paralelas (que se encontram no interior do
ângulo
)
das paralelas (que se encontram no interior do
ângulo