| No do
Passo |
Passo |
Justificativa |
|
01 |
Sejam b e
c as paralelas assintóticas à reta a por P ,
 e e
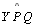 os ângulos de paralelismo, com
os ângulos de paralelismo, com
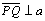 |
Hipótese |
|
02 |
Demonstraremos que
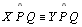 : : |
-
Suponhamos
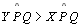
|
Negação da
Tese |
- Tracemos
 tal que tal que
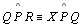
|
|
|
C 04;02.1; construção |
-

|
02.1; 02.2;
P 06 |
-
 está no
interior de está no
interior de
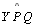
|
02.2, 02.3
|
-
 não é
paralela à reta a por P (b é paralela assintótica e não é
paralela à reta a por P (b é paralela assintótica e
 está 'abaixo' dela, o que significa que
está 'abaixo' dela, o que significa que
 é secante à reta a)
é secante à reta a)
|
01; 02.4;
DH 03 |
-
Prolonguemos
 até
intersectar a reta a no ponto S até
intersectar a reta a no ponto S
|
|
|
02.5;
O 02 ;Ct 01; construção |
- Tomemos
T em a tal que
 e tracemos e tracemos
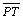
|
|
|
C 01; construção;
I 01 |
-
 ,
pois ,
pois
 (por
construção, passo 02.7), (por
construção, passo 02.7),
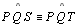 (retos,
pela hipótese e D 13)
e (retos,
pela hipótese e D 13)
e
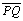 (comum) (comum)
|
02.7; 01;
T 01 (LAL) |
-
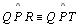
|
02.8 |
-
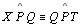
|
02.2; 02.9;
P 01 |
-
Mas

|
P 04 |
-
Contradição. Logo
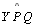 não
é maior que não
é maior que
 . .
|
02.10;
02.11 |
-
Analogamente, supomos
 e
provarmos que e
provarmos que
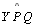 não
é menor que não
é menor que
 ,
sendo portanto congruentes entre si( ,
sendo portanto congruentes entre si(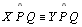 ). ).
|
02.1 a
02.12 |
|
03 |
Demonstraremos que
 e e
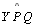 são agudos são agudos |
-
Suponhamos
que
 e e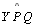 sejam retos
sejam retos
|
Negação da
Tese |
| |
-
As
retas b e c formam uma única reta
-
Mas
b e c são retas distintas (hipótese)
-
Contradição. Logo
 e e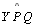 não são retos
não são retos
|
|
|
-
Suponhamos que
 e e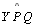 sejam obtusos
sejam obtusos
|
Negação da
Tese |
|
|
a.
Tracemos a reta
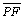 tal que tal que
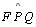 seja
reto.. seja
reto.. |
T 02
|
|
b.
 .
. |
03.2; 03.2.a
e D 08 |
|
c.
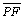 passa
pelo interior do ângulo passa
pelo interior do ângulo
 . . |
03.2.b |
|
d. Logo
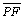 é secante à reta a.
é secante à reta a. |
DH
03 |
|
e. Mas
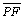 é
paralela à reta a por P. é
paralela à reta a por P. |
03.2.a; T 07, 01 |
|
f.
Contradição. Logo
 e e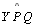 não são obtusos.
não são obtusos. |
03.2.d; 03.2.e |
|
04 |
Portanto
os ângulos
 e e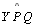 são agudos, uma vez que não são nem retos nem obtusos
são agudos, uma vez que não são nem retos nem obtusos |
03.1.c e
03.2.f |