|
|
Definição
Hiperbólica 07: Um quadrilátero de Lambert é um
quadrilátero que apresenta três ângulos retos. |
|
TH 18: O ângulo não reto de um quadrilátero de Lambert é
agudo,ou seja,
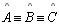 (retos) e
(retos) e
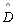 é agudo.
é agudo.
|
|
Demonstração |
Hipótese: Seja □ABCD um quadrilátero de Lambert, com os
ângulos retos
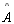 , ,
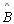 e
e
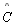 |
|
Tese:
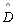 é agudo
é agudo |
| No do
Passo |
Passo |
Justificativa |
| 01 |
|
Construção;
TH 15 ;
D 17 |
| 02 |
Os ângulos
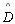 e
e
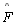 são agudos
são agudos |
TH 17 |
| 03 |
Logo o
quarto ângulo do quadrilátero de Lambert é agudo |
02 |
Os teoremas 19, 20 e 21 serão utilizados nas próximas
demonstrações.
|
|
TH 19: Seja um quadrilátero □ABCD, com
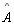 e
e
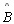 retos e
retos e
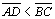 ,
conforme a figura. Nestas condições, temos que ,
conforme a figura. Nestas condições, temos que
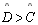
|
|
Demonstração |
Hipótese: Seja □ABCD um quadrilátero, com
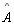 e
e
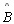 retos e
retos e
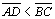 |
|
Tese:
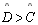 |
| No do
Passo |
Passo |
Justificativa |
| 01 |
Seja um quadrilátero □ABCD, com A e B retos e
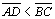 |
Hipótese |
| 02 |
|
T
16; C 01; construção |
| 03 |
□ABED é um quadrilátero de Saccheri |
02;
DH 06 |
| 04 |
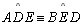 |
03;
TH 15 |
| 05 |
Considerando o triângulo
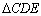 temos que
temos que
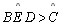 |
T 08 |
| 06 |
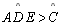 |
4; 5;
P 06 |
| 07 |
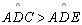 |
P 04 |
| 08 |
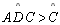 ,
ou ,
ou
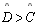 |
06; 07;
P 15 |
Analogamente, podemos provar o teorema 20
| No do
Passo |
Passo |
Justificativa |
| 01 |
Seja um quadrilátero □ABCD, com
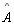 e
e
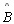 retos e
retos e
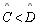 |
Hipótese |
|
02 |
Vamos
supor
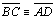 |
Negação da
Tese |
-
□ABCD é um quadrilátero de Saccheri, logo os ângulos
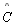 e
e
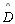 são congruentes e agudos (
são congruentes e agudos (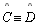 ) )
|
02;
DH 06;
TH 17;
TH 15 |
-
Contradição
|
01; 02.1 |
-
Logo,
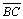 não é congruente a
não é congruente a
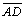
|
02.2 |
| 03 |
Vamos
supor
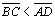 |
Negação da
Tese |
-
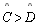
|
TH 19 |
-
Contradição
|
01; 03.1 |
-
Logo,
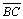 não é menor que
não é menor que
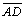
|
03.2 |
| 04 |
Portanto,
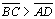 |
02.3; 03.3 |
|
|
TH 22: Seja □ABCD um quadrilátero de Lambert,
com os ângulos retos
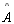 , ,
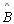 e
e
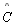 ,
temos que os lados adjacentes à D (ângulo agudo) são maiores que seus
respectivos lados opostos. ,
temos que os lados adjacentes à D (ângulo agudo) são maiores que seus
respectivos lados opostos.
|
| No do
Passo |
Passo |
Justificativa |
| 01 |
Seja □ABCD
um quadrilátero de Lambert, com os ângulos retos
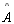 , ,
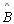 e
e
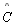 e o ângulo agudo
e o ângulo agudo 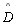 . . |
Hipótese |
|
02 |
Vamos
supor
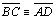 |
Negação da
Tese |
-
□ABCD um
quadrilátero de Saccheri
|
DH 06 |
-
Os ângulos
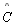 e
e
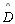 são congruentes e agudos (
são congruentes e agudos (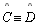 ) )
|
02.1;
TH 15 |
-
Contradição, pois
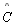 é reto e
é reto e
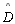 é agudo
é agudo
|
01;02.2;
DH 07 |
-
Logo
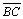 não é congruente a
não é congruente a
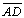
|
02.3 |
| 03 |
Vamos
supor
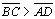 |
Negação da
Tese |
-
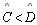
|
TH 20 |
-
Contradição, pois
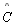 é reto e
é reto e
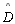 é agudo
é agudo
|
01;
03.1;
DH 07 |
-
Logo
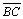 não é maior que
não é maior que
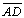
|
03.2 |
| 04 |
Temos
então que
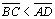 |
02.4; 03.3 |
| 05 |
Analogamente, provamos que
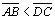 |
01-04 |
|
A partir do estudo do quadrilátero de Lambert, podemos
facilmente provar um teorema que envolve os quadriláteros de Saccheri.
Demonstre o TH 23, construindo o quadrilátero de Lambert a partir do
quadrilátero de Saccheri. |
Resposta |
|
|
TH 23: Seja □ABCD um quadrilátero de Saccheri, de base
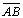 ,
temos que ,
temos que
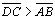 ,
ou seja, o topo é maior que a base ,
ou seja, o topo é maior que a base |
Vamos retomar a atividade 05
e provar o teorema hiperbólico TH 08
|
|
TH 08: A paralela assintótica b, em relação a a, se
aproxima de a, no sentido do paralelismo. |
|
Demonstração |
Hipótese: Seja b uma paralela assintótica à reta a, por P, num
determinado sentido |
|
Tese:
b se aproxima de a no sentido do paralelismo |
| No do
Passo |
Passo |
Justificativa |
| 01 |
Seja b uma
paralela assintótica à reta a, por P, num determinado sentido. Vamos
supor à direita ( o mesmo pode ser provado, supondo à esquerda) |
Hipótese |
| 02 |
|
|
Tomemos três pontos em b, N, M e Q, à direita de
P, tais que N esteja entre P e M e M esteja entre N e Q.
Tracemos por N e M as perpendiculares à reta a
respectivamente por K e L.
Devemos provar que
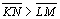 ,
ou seja as retas a e b se aproximam na direção do paralelismo (à
direita) ,
ou seja as retas a e b se aproximam na direção do paralelismo (à
direita) |
|
Construção;
T 16 |
| 03 |
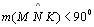 e e
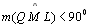 |
TH 03;
DH 04 |
| 04 |
 |
T 03 |
| 05 |
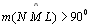 |
03; 04;
P 17 |
| 06 |
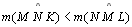 |
03; 05;
P 18 |
| 07 |
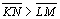 |
TH 21 |
| 08 |
|
|
De modo análogo, devemos completar a demonstração
considerando as perpendiculares em relação à reta b, ou seja, devemos
provar que
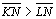 ,
conforme figura. ,
conforme figura. |
|
01-07 |
Após a atividade 8, o Resumo foi atualizado.
 |
Resumo da Geometria
Hiperbólica (RGH) |
|
 .
. .
.