|
A partir das explorações dinâmicas propostas na
seqüência, podemos verificar
alguns dos teoremas sobre as retas hiperbólicas.
obs.: Movimente os pontos P ou P' no semi-plano superior determinado pela reta a.
|
Situação 1: Seja c paralela assintótica à reta a
por um ponto P, à direita. Se
tomarmos um outro ponto qualquer X (à esquerda de P) de c, ou W (à
direita de P), a reta c também será paralela assintótica à reta a por
tais pontos? |
|
|
Observe que por P temos as paralelas assintóticas c e
b em relação à reta a. Por W temos as paralelas assintóticas c e d em
relação à reta a. Por X temos as paralelas assintóticas c e e em relação
à reta a. Podemos então perceber que, como a reta c é paralela
assintótica a reta a à direta, se tomarmos qualquer um dos pontos de c
(W ou X) ela também será paralela assintótica em relação à reta a, por
tais pontos. |
|
|
|
TH 04: Uma reta c paralela assintótica a uma reta a
por um ponto P, num determinado sentido, também o será por qualquer
outro seu ponto (W ou X), no mesmo sentido do paralelismo. |
|
Situação 2: Seja c paralela assintótica à reta a
por um ponto P. A reta a, é também paralela assintótica à reta c por um
seu ponto qualquer R? |
|
|
Sabemos que c é paralela assintótica à reta a por P. Se
tomarmos um ponto qualquer de a, por exemplo o ponto R e traçarmos a
paralela assintótica a c à esquerda, por R, verificaremos que é a própria
reta a. |
|
|
|
TH 05: (simetria do
paralelismo) Se uma reta c é
paralela assintótica a uma
reta a, então a reta a é paralela assintótica à
reta
c. |
|
Situação 3: A reta d é paralela divergente à reta a. A reta a é
paralela divergente à reta d ? |
|
|
Se retomarmos o conceito de
paralelas divergentes,
podemos traçar as paralelas assintóticas (o, p) a d por R e notar que a
reta a está entre tais paralelas limites, sendo portanto paralela
divergente em relação à reta d. |
|
|
|
TH 06: Se uma reta d é
paralela divergente a uma reta
a, então a reta a é paralela divergente à reta d. |
|
Situação 4: A reta c é paralela assintótica (à direita) à reta
a por P. A reta e é paralela assintótica (à direita) à reta a por P'.
As retas c e e são paralelas assintóticas no mesmo sentido do
paralelismo ? |
|
|
Observe que as retas c e e convergem, à direita, para um mesmo
ponto ideal. |
|
|
|
TH 07: (transitividade do paralelismo) Se duas retas c e
e são
paralelas assintóticas
à uma reta a, num determinado sentido,então as retas c e e são paralelas assintóticas entre si, no mesmo sentido. |
|
Situação 5: As retas paralelas
assintóticas se aproximam no sentido do paralelismo ?
obs: Paralelas assintóticas à esquerda: a e b; a e
d; b e d . Paralelas assintótica à direita: a e c; a e e; c e e |
|
|
Analise por exemplo a situação das retas a e b: mova
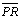 (altura) para a esquerda (sentido do paralelismo de a e b) e verifique que o segmento
(altura) para a esquerda (sentido do paralelismo de a e b) e verifique que o segmento
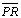 vai diminuindo a
medida que nos aproximamos da circunferência limite, ou seja, diminuir a distância entre as retas significa que as retas vão se aproximando. vai diminuindo a
medida que nos aproximamos da circunferência limite, ou seja, diminuir a distância entre as retas significa que as retas vão se aproximando. |
|
|
|
TH 08: A paralela assintótica
b, em relação à reta a, se
aproxima de a, no sentido do paralelismo. |
|
Situação 6: As retas a e d são paralelas divergentes. Movimente
o ponto T pela reta d. A reta e é perpendicular à reta d. A reta
f é perpendicular às retas a e d.
É possível
que
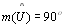 e as retas e e f sejam distintas? Ou seja é possível que duas retas
divergentes apresentem mais de uma perpendicular comum ?
e as retas e e f sejam distintas? Ou seja é possível que duas retas
divergentes apresentem mais de uma perpendicular comum ? |
|
|
Movimentando a reta e podemos perceber que somente
quando ela coincide com a reta f é que e torna-se perpendicular as
retas a e d, ou seja a perpendicular é única. |
|
|
|
TH 09: Duas
paralelas divergentes apresentam uma única
perpendicular comum. |
|
Um dos teoremas acima, o TH 08 será
demonstrado nas próximas atividades. Demonstre o próximo teorema
utilizando um dos teoremas apresentados nessa atividade. Lembre-se de
analisar as possibilidades das retas no plano hiperbólico.
Após a atividade 5, o Resumo foi atualizado.
 |
Resumo da Geometria
Hiperbólica (RGH) |
|
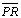 vai diminuindo a
medida que nos aproximamos da circunferência limite, ou seja, diminuir a distância entre as retas significa que as retas vão se aproximando.
vai diminuindo a
medida que nos aproximamos da circunferência limite, ou seja, diminuir a distância entre as retas significa que as retas vão se aproximando.