|
Construa uma circunferência que passe por três pontos
dados do plano.
|
|
|
|
|
Na geometria euclidiana sabemos que três pontos não
colineares determinam uma circunferência. Na geometria hiperbólica essa
condição não é mais suficiente, além de que os três pontos devam pertencer
ao plano de Poincaré.
Na geometria hiperbólica há outros lugares geométricos
além da circunferência, que também poderão ser determinados por três pontos.
Veremos tais situações na próxima atividade.
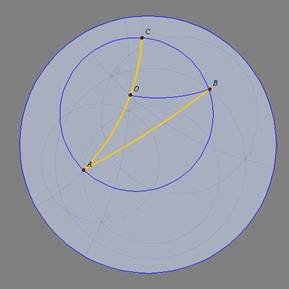
Analisaremos nessa atividade um conhecido teorema sobre o
ângulo inscrito numa circunferência.
|
TH 28: A medida de um
ângulo inscrito num círculo é menor do que a metade da medida do ângulo
central correspondente. Temos que considerar três casos:
|
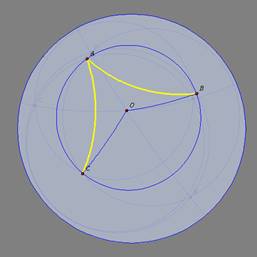
| 1o caso: O
é interno ao ângulo |
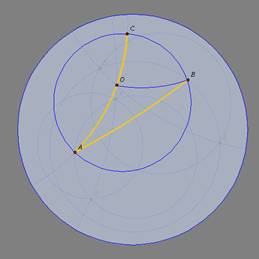
2o caso: O
está num lado do ângulo |
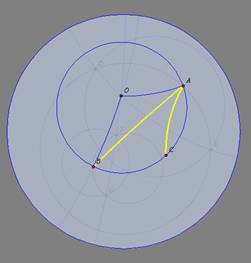
3o caso: O
é externo ao ângulo |
|
 |
 |
 |
|
Demonstração |
Hipótese: Dado o ângulo
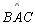 inscrito na circunferência de centro O e de ângulo central
inscrito na circunferência de centro O e de ângulo central
 |
|
Tese: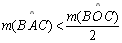 |
| No do
Passo |
Passo |
Justificativa |
| 01 |
Dado um
ângulo
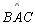 inscrito na circunferência de centro O, de ângulo central
inscrito na circunferência de centro O, de ângulo central
 |
Hipótese |
| |
1o
caso: O é interno ao ângulo |
| 02 |
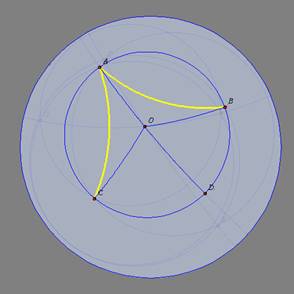 |
Tracemos o diâmetro por A,
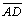 . . |
|
Construção |
| 03 |
O ângulo
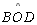 é externo ao
é externo ao
 ,
sendo portando maior que a soma das medidas dos ângulos não adjacentes,
ou seja, ,
sendo portando maior que a soma das medidas dos ângulos não adjacentes,
ou seja,
 |
TH 27;
D 09 |
| 04 |
Como
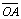 e
e
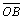 são raios, temos que
são raios, temos que
 é isósceles e
é isósceles e
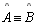 |
01;
D 16 |
| 05 |
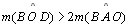 |
03; 04 |
| 06 |
Da mesma
forma, considerando
 ,
temos que ,
temos que
 |
03-05 |
| 07 |
Somando
ambos os membros, temos:
 |
05; 06 |
|
08 |
2o
caso: O está num lado do ângulo |
|
 |
O
ângulo
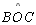 é externo ao triângulo
é externo ao triângulo
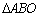 . .
 |
|
D 09;03-07 |
|
09 |
3o
caso: O é externo ao ângulo |
|
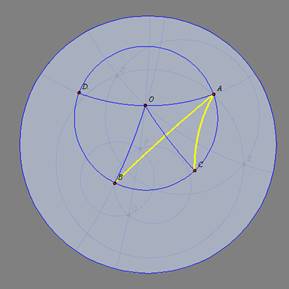 |
Tracemos o diâmetro
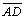 e o raio
e o raio
 .Considerando
o 2o caso, temos: .Considerando
o 2o caso, temos:
|
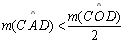 |
 |
|
Subtraindo as inequações:
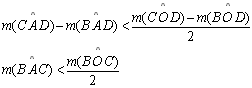 |
|
|
07; 08 |
Obs: se o centro do disco de Poincaré não for
interior ao ângulo, não é possível estabelecer uma relação com o respectivo
ângulo central, ou seja, "a medida de um ângulo inscrito em um
arco varia quando o vértice varia sua posição (01)".
|
Analise a seguinte situação: |
|
|
Dada uma reta secante a uma circunferência nos pontos P e Q,
que não passa pelo seu centro O. Sendo M o ponto médio de
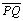 , temos que a reta , temos que a reta
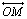 é perpendicular à
secante é perpendicular à
secante 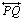 . .
|
|
Esse também é um conhecido teorema sobre as posições relativas de
reta e circunferência da geometria euclidiana. Ele vale também na
geometria hiperbólica?
Justifique sua resposta. |
Resposta |
Após a atividade 10, o Resumo foi atualizado.
 |
Resumo da Geometria
Hiperbólica (RGH) |
|








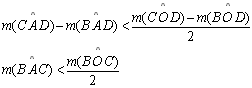
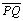 , temos que a reta
, temos que a reta
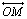 é perpendicular à
secante
é perpendicular à
secante 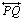 .
.