|
Introdução: Explicando o Software Cinderella e as atividades propostas |
|||||||||||||||||||||||||||||||||||||||||||||||||
|
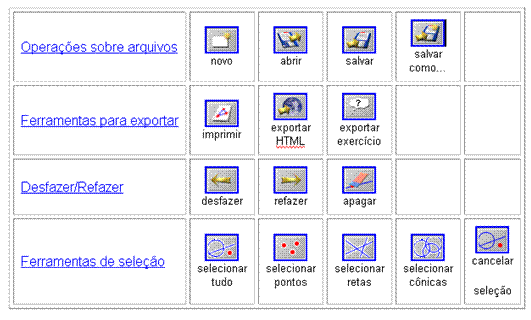
SOFTWARE CINDERELLA O Cinderella é um software de geometria dinâmica de utilização intuitiva. Uma de suas particularidades é a possibilidade de explorar uma mesma construção geométrica em geometrias diferentes (euclidiana, hiperbólica e esférica). Não faremos uma apresentação detalhada do seus recursos, mas nos deteremos nas ferramentas necessárias à resolução das atividades que serão propostas. Apresentaremos a seguir o menu completo. Como ferramentas gerais ele apresenta:
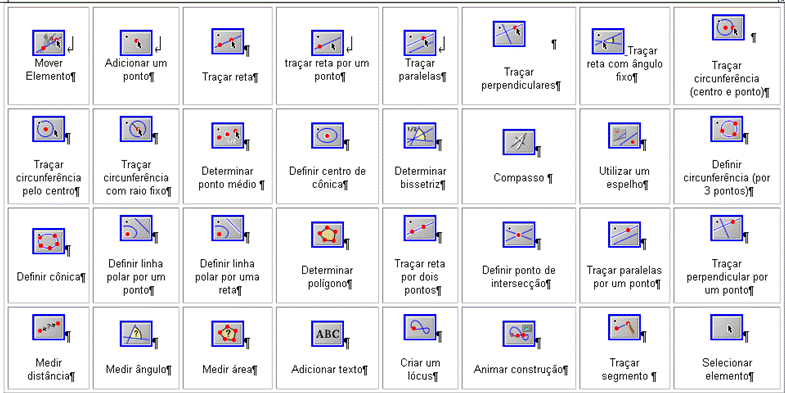
As demais ferramentas se encontram abaixo relacionadas:
SEQÜÊNCIA DIDÁTICA As atividades propostas apresentam alguns momentos, a saber:
As construções foram previamente elaboradas e são apresentadas em conjunto com uma questão investigativa. Espera-se que o aprendiz 'movimente' os objetos livres da construção a fim de observar o comportamento da figura, conjecture e formule uma resposta à questão proposta.
Propomos alguns exercícios de construção geométrica, em que são apresentados uma barra
simplificada de
ferramentas, contendo os ícones que poderão ser utilizados na resolução da
atividade, além dos quatro ícones padrão (
Os alunos podem elaborar a construção, selecionando um dos ícones do menu e executando a
sua respectiva ação. Caso o aluno apresente alguma dificuldade no
desenvolvimento da construção,
poderá verificar através do ícone
No final desta atividade de introdução, propomos um exemplo prático, possibilitando uma familiarização com o software.
No decorrer das seqüências as definições de alguns termos, não listados na geometria absoluta, serão apresentados na medida em que se fizerem necessários, dando continuidade à exposição da geometria hiperbólica.
Em algumas situações as demonstrações são apresentadas e em outras o aluno é convidado a elaborá-las. Adotamos a apresentação das demonstrações em três colunas (número do passo, passo e justificativa) e explicitamos a hipótese e a tese envolvidas. Os passos de construções geométricas são justificados como 'construção', pois estamos assumindo a possibilidade de construção de ponto, retas, segmentos, paralelas, perpendiculares, triângulos, quadriláteros e circunferências nessa geometria.
Inserimos algumas situações de reflexão. Esperamos que o aluno possa, resgatando seus conhecimentos anteriores da geometria euclidiana e considerando os tópicos apresentados até a respectiva atividade, concluir com sucesso a resposta da situação apresentada.
No final de cada atividade, as definições e os teoremas estudados foram acrescentados ao Resumo da Geometria Hiperbólica (RGH), que é uma lista dos axiomas válidos, das definições e dos teoremas até então estudados, que estarão disponíveis para as demonstrações futuras. No término das seqüência didática o RGH conterá todos os itens estudados.
As eventuais dúvidas sobre a apresentação das definições ou demonstrações apresentadas no decorrer das atividades devem ser expostas pelo correio eletrônico. Ressaltamos a importância de se relatar tais dificuldades para o desenvolvimento da pesquisa. Espera-se que o aluno, ao questionar uma demonstrações identifique quais os passos não compreendidos. É fundamental que, para as demonstrações por ele elaboradas, mesmo que não concluídas, sejam entregues com os passos que foram possíveis executar. Tal material nos será particularmente útil nas investigações de nossas hipóteses. Após a entrega das atividades, feitas pelo correio eletrônico, enviaremos a resposta e posteriormente as resoluções serão comentadas. Essa disponibilização das soluções possibilitará ao aluno a revisão das estratégias adotadas, uma reflexão e uma eventual retomada dos tópicos propostos, dando continuidade aos seus estudos.
UTILIZANDO O SOFTWARE Caso você não tenha experiência com o Cinderella ou com algum outro software de geometria dinâmica elaboramos uma atividade de familiarização, com duas construções geométricas. Nessa atividade explicitamos uma rotina de passos para a execução da tarefa.
Caso julgue desnecessário realizar tais construções, prossiga a sua leitura. O compasso ideal (
Para exemplificar, propomos um exercício de construção geométrica, utilizando algumas das ferramentas disponíveis. Leia atentamente as instruções dadas em exercícios interativos.
Selecione as ferramentas no menu
simplificado para executar a construção. Lembre-se: no caso de dúvida, o
ícone
Após a construção, ela será apresentada no plano euclidiano e também plano hiperbólico
(que será melhor detalhado na atividade 2). Movimente, utilizando o ícone
Vista Hiperbólica - Modelo de Poincaré
NOTAÇÕES Para melhor esclarecimento, listamos abaixo as notações utilizadas na seqüência didática:
BIBLIOGRAFIA Para a realização das atividades utilizamos a seguinte bibliografia: AGAZZI, Evandro; PALLADINO, Dario. Le geometrie non euclidee e i fondamenti della geometria dal punto de vista elementare. Brescia: La Scuola. 1998. 342 p. BARBOSA, João Lucas, M. Geometria Hiperbólica, Rio de Janeiro: IMPA, 1985. 167p. COUTINHO, Lázaro. Convite às Geometrias não-Euclidianas. Rio de Janeiro: ed. Interciência. 2001. 114p. DOLCE, O.; POMPEU, J.N. Fundamentos de Matemática Elementar. Geometria Plana. 7. ed. São Paulo: Atual. 1993. 451p. v.9. HILBERT, David. Fundamentos da Geometria. Coord. A. J. Franco de Oliveira. Lisboa: ed. Gradiva. 2003. 338 p. LINS, Geraldo H. B. Introdução à Geometria Hiperbólica: Semelhanças e Diferenças. 2002. 200 f. Dissertação (Mestrado em Matemática Aplicada) - Universidade Federal do Rio de Janeiro, Rio de Janeiro. TERDIMAN, Esther Wajskop. A geometria hiperbólica e sua consistência. 1989. 203 f. Dissertação (Mestrado em Matemática). Pontifícia Universidade Católica, São Paulo. TRUDEAU, Richard. La revoluzione non euclidia. Tradução Alberto Albano, Carla Marchisepppe e Tullio Cannillo. 2 ed. Torino: ed. Bollati Boringhieri. 2004. 280 p. obs: as fotos foram extraídas dos sites: http://www.profcardy.com/matematicos http://www-groups.dcs.st-and.ac.uk/~history/BiogIndex.html
|
poderá sugerir alguns passos; selecione cada ferramenta no menu antes de
executar a sua ação; para recomeçar a construção utilize o ícone
. 
, 
);
por três de seus pontos (ABF)
)
)
);por
um ponto de uma de suas semi-retas, o vértice e um ponto de sua outra
semi-reta (
);
por uma de suas retas, o vértice e um ponto de sua outra semi-reta (
)
; □ABCD)
║
